Question Number 106932 by Ar Brandon last updated on 07/Aug/20
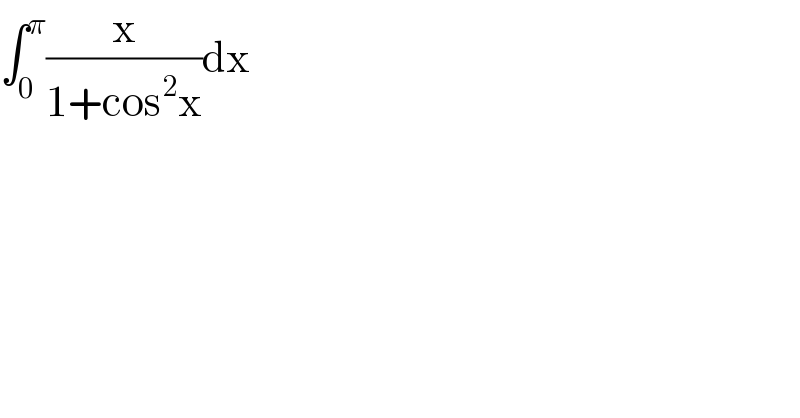
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 08/Aug/20
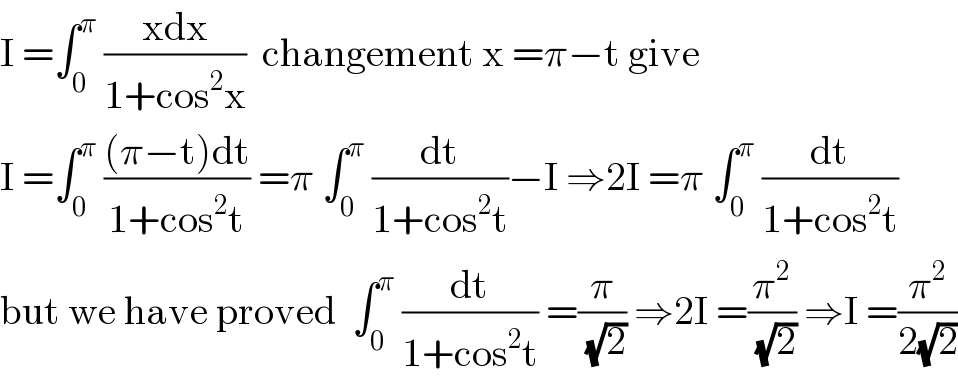
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{xdx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\:\mathrm{changement}\:\mathrm{x}\:=\pi−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{\left(\pi−\mathrm{t}\right)\mathrm{dt}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\:=\pi\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{t}}−\mathrm{I}\:\Rightarrow\mathrm{2I}\:=\pi\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{t}} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{have}\:\mathrm{proved}\:\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{2I}\:=\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}}\:\Rightarrow\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 08/Aug/20
![∫_0 ^π (x/(1+cos^2 x))=∫((π−x)/(1+cos^2 x))=I 2I=∫_0 ^π (π/(1+cos^2 x)) 2I=π∫_0 ^π ((sec^2 x)/(sec^2 x+1)) 2I=π∫_0 ^π (dt/(t^2 +2)) (tanx=t 2I=(π/( (√2)))[tan^(−1) (((tanx)/( (√2))))]_0 ^π =(π/( (√2))).π=(π^2 /( (√2))) I=(π^2 /(2(√2)))](https://www.tinkutara.com/question/Q106994.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{{x}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}=\int\frac{\pi−{x}}{\mathrm{1}+{cos}^{\mathrm{2}} {x}}={I} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+{cos}^{\mathrm{2}} {x}} \\ $$$$\mathrm{2}{I}=\pi\int_{\mathrm{0}} ^{\pi} \frac{{sec}^{\mathrm{2}} {x}}{{sec}^{\mathrm{2}} {x}+\mathrm{1}} \\ $$$$\mathrm{2}{I}=\pi\int_{\mathrm{0}} ^{\pi} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\left({tanx}={t}\right. \\ $$$$\mathrm{2}{I}=\frac{\pi}{\:\sqrt{\mathrm{2}}}\left[{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\pi} =\frac{\pi}{\:\sqrt{\mathrm{2}}}.\pi=\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}} \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Commented by Ar Brandon last updated on 08/Aug/20
������
Answered by Ar Brandon last updated on 08/Aug/20
![J=∫_0 ^π (x/(1+cos^2 x))dx =∫_0 ^π ((π−x)/(1+cos^2 x))dx=∫_0 ^π (π/(1+cos^2 x))dx−J 2J=∫_0 ^π (π/(1+cos^2 x))dx=π∫_0 ^π ((sec^2 x)/(sec^2 x+1))dx =π∫_0 ^π ((sec^2 x)/(tan^2 x+2))dx=π∫_0 ^π ((d(tanx))/(tan^2 x+2))dx =π[(1/( (√2)))Arctan(((tanx)/( (√2))))]_0 ^π =(π/( (√2)))[Arctan(−(0/( (√2))))−Arctan((0/( (√2))) )]=((π(π−0))/( (√2)))=(π^2 /( (√2))) J=(π^2 /(2(√2)))](https://www.tinkutara.com/question/Q106999.png)
$$\mathcal{J}=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\pi} \frac{\pi−\mathrm{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}−\mathcal{J} \\ $$$$\mathrm{2}\mathcal{J}=\int_{\mathrm{0}} ^{\pi} \frac{\pi}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}=\pi\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{sec}^{\mathrm{2}} \mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:=\pi\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sec}^{\mathrm{2}} \mathrm{x}}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{2}}\mathrm{dx}=\pi\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\left(\mathrm{tanx}\right)}{\mathrm{tan}^{\mathrm{2}} \mathrm{x}+\mathrm{2}}\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:=\pi\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{Arctan}\left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\pi} \\ $$$$\:\:\:\:\:\:\:=\frac{\pi}{\:\sqrt{\mathrm{2}}}\left[\mathrm{Arctan}\left(−\frac{\mathrm{0}}{\:\sqrt{\mathrm{2}}}\right)−\mathrm{Arctan}\left(\frac{\mathrm{0}}{\:\sqrt{\mathrm{2}}}\:\right)\right]=\frac{\pi\left(\pi−\mathrm{0}\right)}{\:\sqrt{\mathrm{2}}}=\frac{\pi^{\mathrm{2}} }{\:\sqrt{\mathrm{2}}} \\ $$$$\mathcal{J}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
