Question Number 172545 by SANOGO last updated on 28/Jun/22
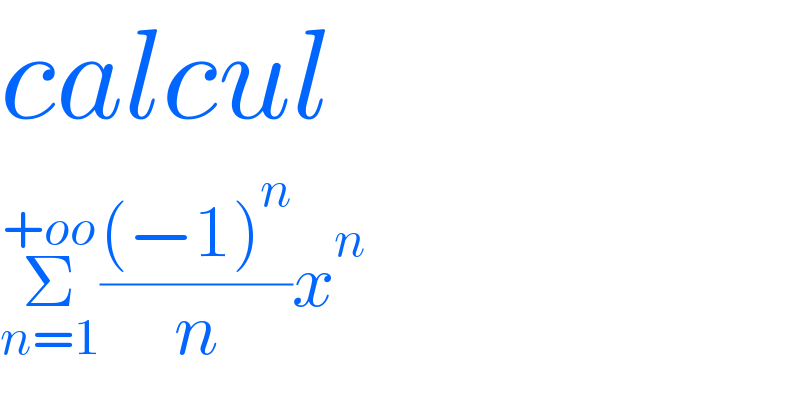
$${calcul} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}{x}^{{n}} \\ $$
Commented by mr W last updated on 28/Jun/22
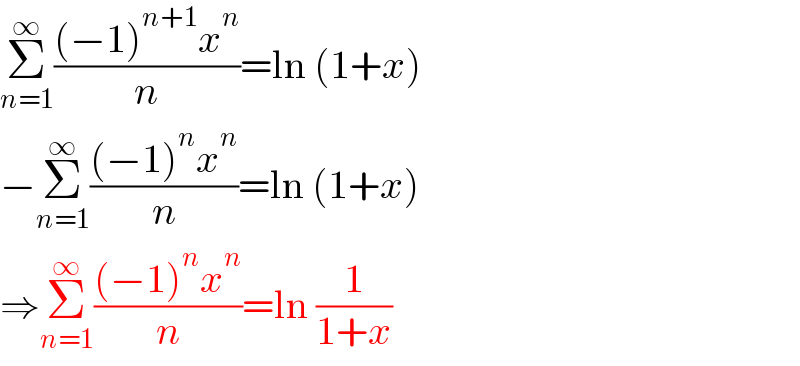
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} }{{n}}=\mathrm{ln}\:\left(\mathrm{1}+{x}\right) \\ $$$$−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} }{{n}}=\mathrm{ln}\:\left(\mathrm{1}+{x}\right) \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} }{{n}}=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}+{x}} \\ $$
Answered by Jamshidbek last updated on 28/Jun/22

$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} +…=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \centerdot\mathrm{x}^{\mathrm{n}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \centerdot\mathrm{x}^{\mathrm{n}} \:\:\:\:\:\mid\mathrm{x}\mid<\mathrm{1} \\ $$$$\mathrm{integrate}\:\mathrm{both}\:\mathrm{side} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \centerdot\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \centerdot\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}} \\ $$$$−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)=\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}} \centerdot\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\:\:\:\mid\mathrm{x}\mid<\mathrm{1} \\ $$$$\mathrm{Telegram}:@\mathrm{math\_undergraduate} \\ $$$$ \\ $$
