Question Number 172599 by Mikenice last updated on 29/Jun/22

Answered by Rasheed.Sindhi last updated on 29/Jun/22
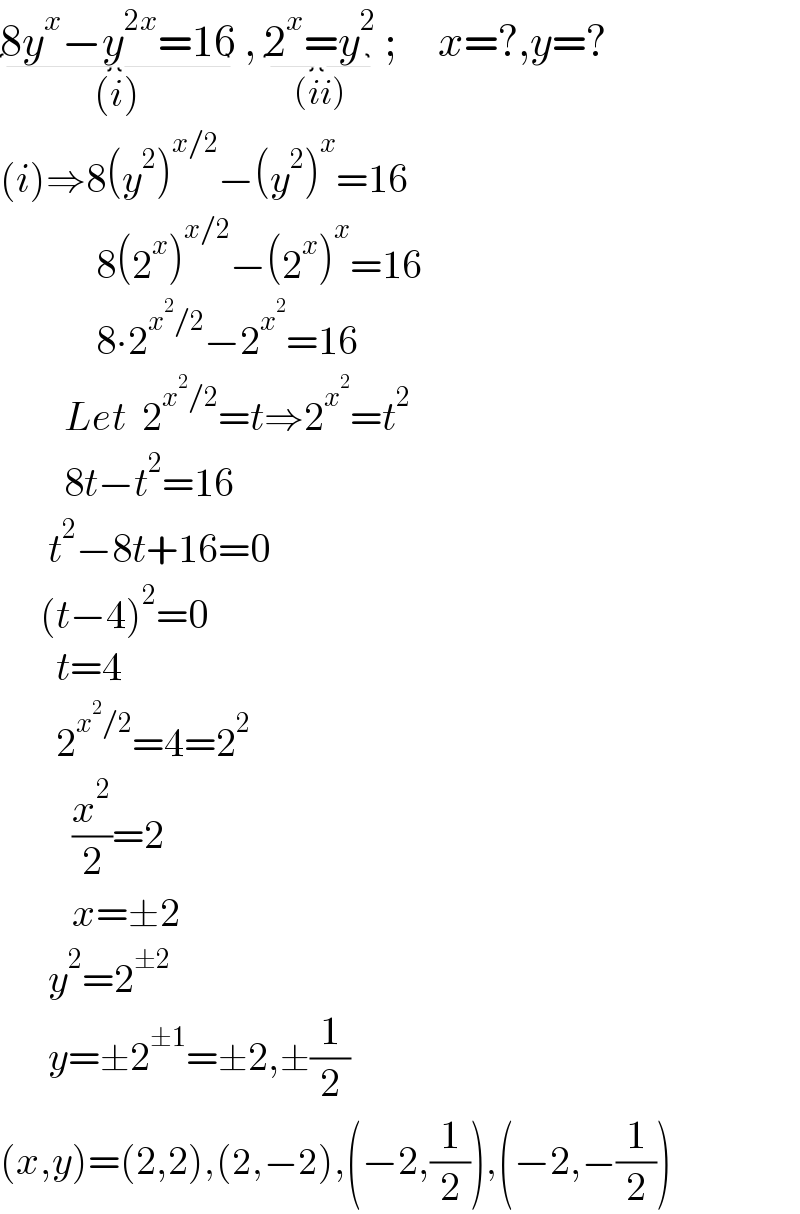
$$\underset{\left({i}\right)} {\underbrace{\mathrm{8}{y}^{{x}} −{y}^{\mathrm{2}{x}} =\mathrm{16}}}\:,\:\underset{\left({ii}\right)} {\underbrace{\mathrm{2}^{{x}} ={y}^{\mathrm{2}} }}\:;\:\:\:\:\:{x}=?,{y}=? \\ $$$$\left({i}\right)\Rightarrow\mathrm{8}\left({y}^{\mathrm{2}} \right)^{{x}/\mathrm{2}} −\left({y}^{\mathrm{2}} \right)^{{x}} =\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\left(\mathrm{2}^{{x}} \right)^{{x}/\mathrm{2}} −\left(\mathrm{2}^{{x}} \right)^{{x}} =\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}\centerdot\mathrm{2}^{{x}^{\mathrm{2}} /\mathrm{2}} −\mathrm{2}^{{x}^{\mathrm{2}} } =\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:{Let}\:\:\mathrm{2}^{{x}^{\mathrm{2}} /\mathrm{2}} ={t}\Rightarrow\mathrm{2}^{{x}^{\mathrm{2}} } ={t}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{8}{t}−{t}^{\mathrm{2}} =\mathrm{16} \\ $$$$\:\:\:\:\:\:{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{16}=\mathrm{0} \\ $$$$\:\:\:\:\:\left({t}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{t}=\mathrm{4} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}^{{x}^{\mathrm{2}} /\mathrm{2}} =\mathrm{4}=\mathrm{2}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:{x}=\pm\mathrm{2} \\ $$$$\:\:\:\:\:\:{y}^{\mathrm{2}} =\mathrm{2}^{\pm\mathrm{2}} \\ $$$$\:\:\:\:\:\:{y}=\pm\mathrm{2}^{\pm\mathrm{1}} =\pm\mathrm{2},\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left({x},{y}\right)=\left(\mathrm{2},\mathrm{2}\right),\left(\mathrm{2},−\mathrm{2}\right),\left(−\mathrm{2},\frac{\mathrm{1}}{\mathrm{2}}\right),\left(−\mathrm{2},−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by Tawa11 last updated on 30/Jun/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Rasheed.Sindhi last updated on 30/Jun/22

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{miss}}! \\ $$
