y-y-1-cosx-

Question Number 107108 by Ar Brandon last updated on 08/Aug/20

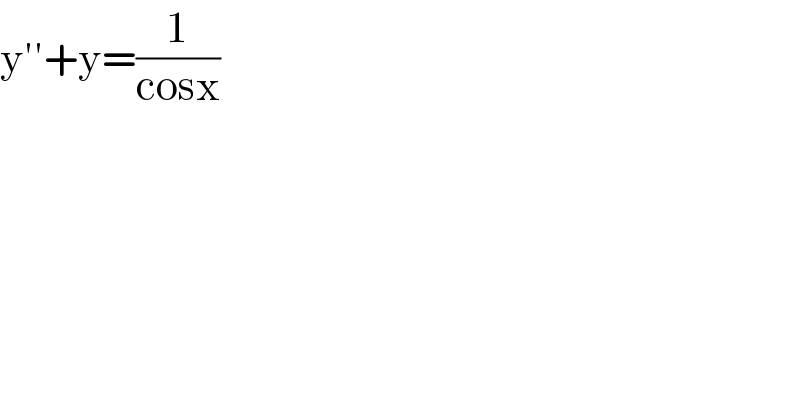
$$\mathrm{y}''+\mathrm{y}=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$

Commented by mohammad17 last updated on 08/Aug/20

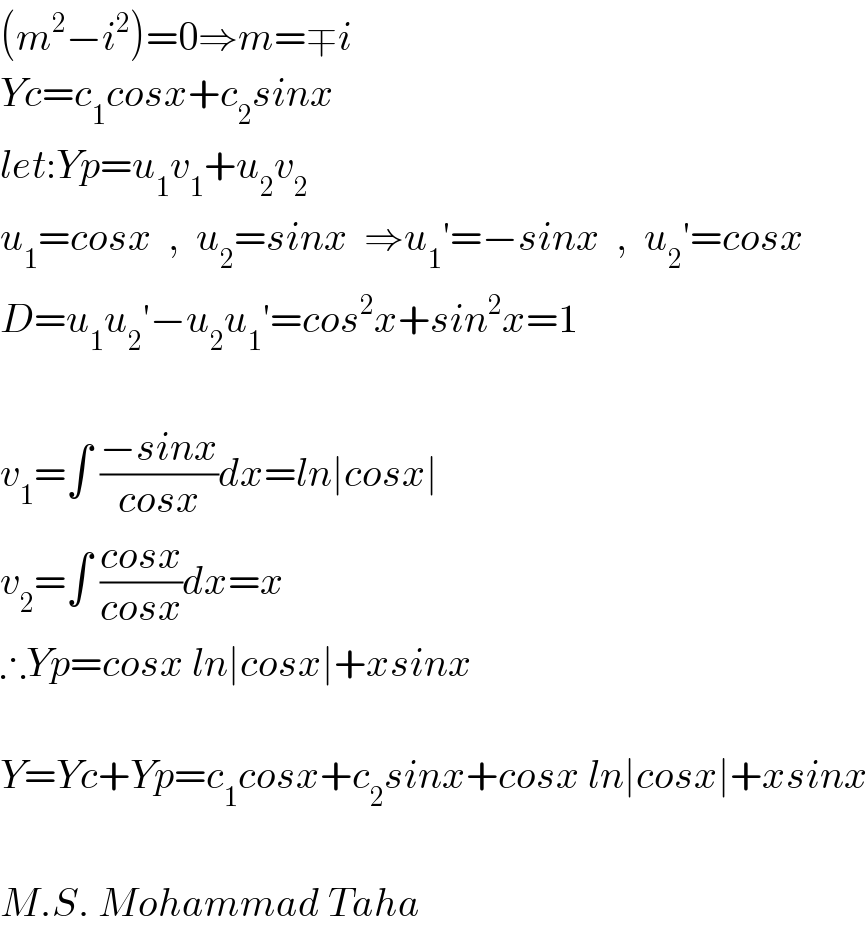
(m^2 −i^2 )=0⇒m=∓i Yc=c_1 cosx+c_2 sinx let:Yp=u_1 v_1 +u_2 v_2 u_1 =cosx , u_2 =sinx ⇒u_1 ′=−sinx , u_2 ′=cosx D=u_1 u_2 ′−u_2 u_1 ′=cos^2 x+sin^2 x=1 v_1 =∫ ((−sinx)/(cosx))dx=ln∣cosx∣ v_2 =∫ ((cosx)/(cosx))dx=x ∴Yp=cosx ln∣cosx∣+xsinx Y=Yc+Yp=c_1 cosx+c_2 sinx+cosx ln∣cosx∣+xsinx M.S. Mohammad Taha

$$\left({m}^{\mathrm{2}} −{i}^{\mathrm{2}} \right)=\mathrm{0}\Rightarrow{m}=\mp{i} \\ $$$${Yc}={c}_{\mathrm{1}} {cosx}+{c}_{\mathrm{2}} {sinx} \\ $$$${let}:{Yp}={u}_{\mathrm{1}} {v}_{\mathrm{1}} +{u}_{\mathrm{2}} {v}_{\mathrm{2}} \\ $$$${u}_{\mathrm{1}} ={cosx}\:\:,\:\:{u}_{\mathrm{2}} ={sinx}\:\:\Rightarrow{u}_{\mathrm{1}} '=−{sinx}\:\:,\:\:{u}_{\mathrm{2}} '={cosx} \\ $$$${D}={u}_{\mathrm{1}} {u}_{\mathrm{2}} '−{u}_{\mathrm{2}} {u}_{\mathrm{1}} '={cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}=\mathrm{1} \\ $$$$ \\ $$$${v}_{\mathrm{1}} =\int\:\frac{−{sinx}}{{cosx}}{dx}={ln}\mid{cosx}\mid \\ $$$${v}_{\mathrm{2}} =\int\:\frac{{cosx}}{{cosx}}{dx}={x} \\ $$$$\therefore{Yp}={cosx}\:{ln}\mid{cosx}\mid+{xsinx} \\ $$$$ \\ $$$${Y}={Yc}+{Yp}={c}_{\mathrm{1}} {cosx}+{c}_{\mathrm{2}} {sinx}+{cosx}\:{ln}\mid{cosx}\mid+{xsinx} \\ $$$$ \\ $$$${M}.{S}.\:{Mohammad}\:{Taha} \\ $$

Commented by Ar Brandon last updated on 08/Aug/20

Thanks��

Commented by mohammad17 last updated on 08/Aug/20

$${welcome} \\ $$

Answered by mathmax by abdo last updated on 08/Aug/20

y^(′′) +y =(1/(cosx)) h→y^(′′) +y=0⇒r^2 +1 =0 ⇒r =+^− 1 ⇒y_h =acosx +bsinx=au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((cosx sinx)),((−sinx cosx)))=cos^2 x +sin^2 x=1 W_1 = determinant (((0 sinx)),(((1/(cosx)) cosx)))=−((sinx)/(cosx)) W_2 = determinant (((cosx 0)),((−sinx (1/(cosx)))))= 1 v_1 =∫ (w_1 /w)dx =−∫ ((sinx)/(cosx))dx =ln∣cosx∣ v_2 =∫ (w_2 /w)dx =∫ dx =x ⇒y_p =u_1 v_1 +u_2 v_2 =cosxln∣cosx∣ +xsinx the general solution is y =y_h +y_p ⇒y =cosxln∣cosx∣ +xsinx +acosx +bsinx

$$\mathrm{y}^{''} +\mathrm{y}\:=\frac{\mathrm{1}}{\mathrm{cosx}} \\ $$$$\mathrm{h}\rightarrow\mathrm{y}^{''} \:+\mathrm{y}=\mathrm{0}\Rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{1}\:\Rightarrow\mathrm{y}_{\mathrm{h}} =\mathrm{acosx}\:+\mathrm{bsinx}=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{cosx}\:\:\:\:\:\:\:\:\:\:\mathrm{sinx}}\\{−\mathrm{sinx}\:\:\:\:\:\:\:\:\mathrm{cosx}}\end{vmatrix}=\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}=\mathrm{1} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sinx}}\\{\frac{\mathrm{1}}{\mathrm{cosx}}\:\:\:\:\:\:\:\:\:\mathrm{cosx}}\end{vmatrix}=−\frac{\mathrm{sinx}}{\mathrm{cosx}} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cosx}\:\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{sinx}\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{cosx}}}\end{vmatrix}=\:\mathrm{1} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\frac{\mathrm{sinx}}{\mathrm{cosx}}\mathrm{dx}\:=\mathrm{ln}\mid\mathrm{cosx}\mid \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\:\mathrm{dx}\:=\mathrm{x}\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} =\mathrm{cosxln}\mid\mathrm{cosx}\mid\:+\mathrm{xsinx}\: \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} \\ $$$$\Rightarrow\mathrm{y}\:=\mathrm{cosxln}\mid\mathrm{cosx}\mid\:+\mathrm{xsinx}\:+\mathrm{acosx}\:+\mathrm{bsinx} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply