Question Number 41622 by math khazana by abdo last updated on 10/Aug/18
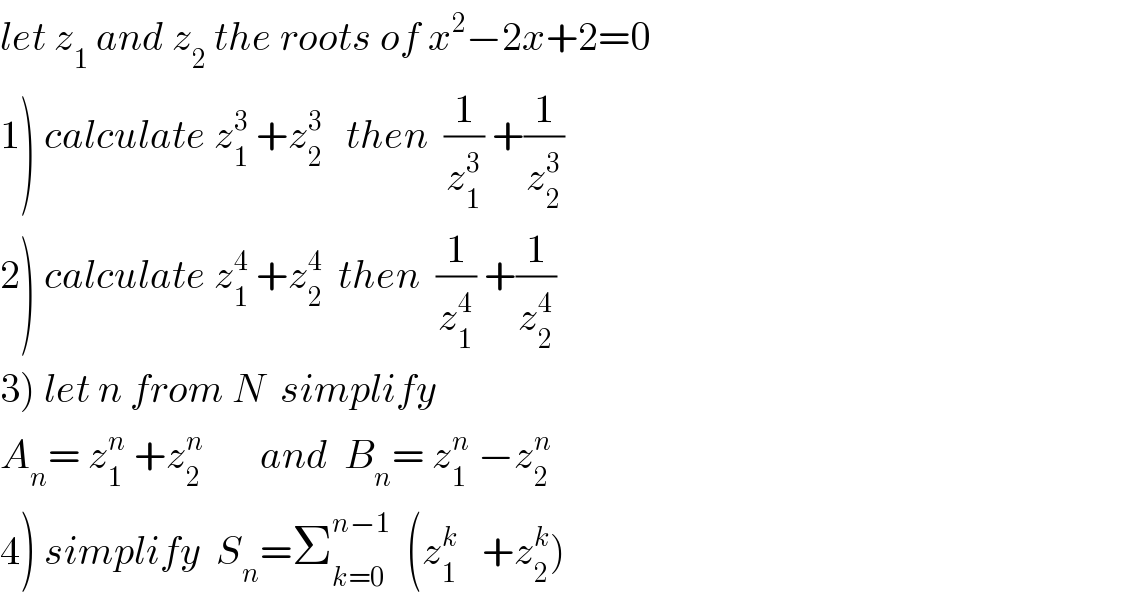
$${let}\:{z}_{\mathrm{1}} \:{and}\:{z}_{\mathrm{2}} \:{the}\:{roots}\:{of}\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{z}_{\mathrm{1}} ^{\mathrm{3}} \:+{z}_{\mathrm{2}} ^{\mathrm{3}} \:\:\:{then}\:\:\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{3}} }\:+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{3}} } \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{z}_{\mathrm{1}} ^{\mathrm{4}} \:+{z}_{\mathrm{2}} ^{\mathrm{4}} \:\:{then}\:\:\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{4}} }\:+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{4}} } \\ $$$$\left.\mathrm{3}\right)\:{let}\:{n}\:{from}\:{N}\:\:{simplify} \\ $$$${A}_{{n}} =\:{z}_{\mathrm{1}} ^{{n}} \:+{z}_{\mathrm{2}} ^{{n}} \:\:\:\:\:\:\:{and}\:\:{B}_{{n}} =\:{z}_{\mathrm{1}} ^{{n}} \:−{z}_{\mathrm{2}} ^{{n}} \\ $$$$\left.\mathrm{4}\right)\:{simplify}\:\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\left({z}_{\mathrm{1}} ^{{k}} \:\:\:+{z}_{\mathrm{2}} ^{{k}} \right) \\ $$
Commented by rahul 19 last updated on 10/Aug/18
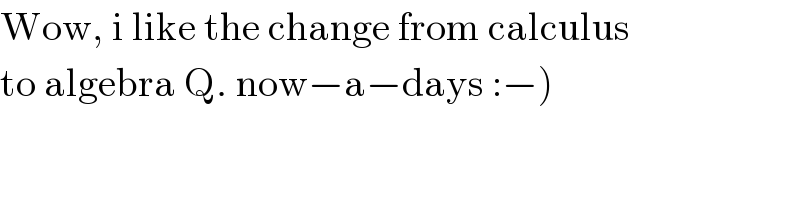
$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{like}\:\mathrm{the}\:\mathrm{change}\:\mathrm{from}\:\mathrm{calculus} \\ $$$$\left.\mathrm{to}\:\mathrm{algebra}\:\mathrm{Q}.\:\mathrm{now}−\mathrm{a}−\mathrm{days}\::−\right) \\ $$
Commented by alex041103 last updated on 10/Aug/18

$$:\mathrm{D} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
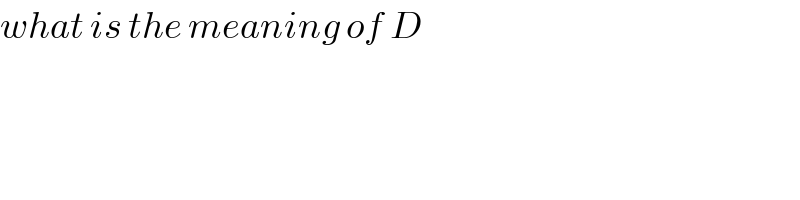
$${what}\:{is}\:{the}\:{meaning}\:{of}\:{D} \\ $$
Commented by alex041103 last updated on 10/Aug/18

$${Its}\:{like}\:\:{big}\:{smile}\:{if}\:{you}\:{rotate}\:{D}\:\mathrm{90}° \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18

$${ha}\:{ha}\:{ha}… \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
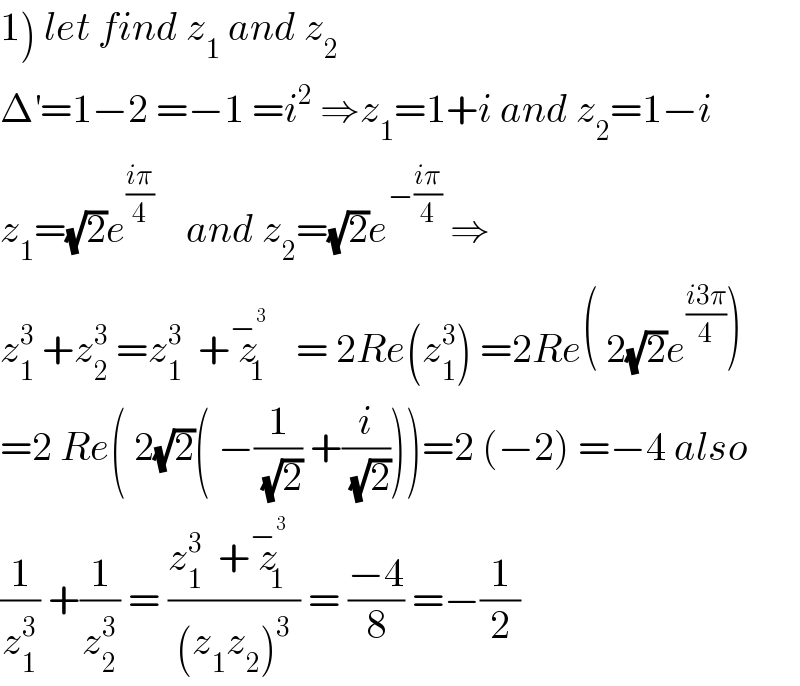
$$\left.\mathrm{1}\right)\:{let}\:{find}\:{z}_{\mathrm{1}} \:{and}\:{z}_{\mathrm{2}} \\ $$$$\Delta^{'} =\mathrm{1}−\mathrm{2}\:=−\mathrm{1}\:={i}^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\mathrm{1}+{i}\:{and}\:{z}_{\mathrm{2}} =\mathrm{1}−{i} \\ $$$${z}_{\mathrm{1}} =\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:\:\:{and}\:{z}_{\mathrm{2}} =\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$${z}_{\mathrm{1}} ^{\mathrm{3}} \:+{z}_{\mathrm{2}} ^{\mathrm{3}} \:={z}_{\mathrm{1}} ^{\mathrm{3}} \:\:+\overset{−^{\mathrm{3}} } {{z}}_{\mathrm{1}} \:\:=\:\mathrm{2}{Re}\left({z}_{\mathrm{1}} ^{\mathrm{3}} \right)\:=\mathrm{2}{Re}\left(\:\mathrm{2}\sqrt{\mathrm{2}}{e}^{\frac{{i}\mathrm{3}\pi}{\mathrm{4}}} \right) \\ $$$$=\mathrm{2}\:{Re}\left(\:\mathrm{2}\sqrt{\mathrm{2}}\left(\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\right)=\mathrm{2}\:\left(−\mathrm{2}\right)\:=−\mathrm{4}\:{also} \\ $$$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{3}} }\:+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{3}} }\:=\:\frac{{z}_{\mathrm{1}} ^{\mathrm{3}} \:\:+\overset{−^{\mathrm{3}} } {{z}}_{\mathrm{1}} }{\left({z}_{\mathrm{1}} {z}_{\mathrm{2}} \right)^{\mathrm{3}} }\:=\:\frac{−\mathrm{4}}{\mathrm{8}}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
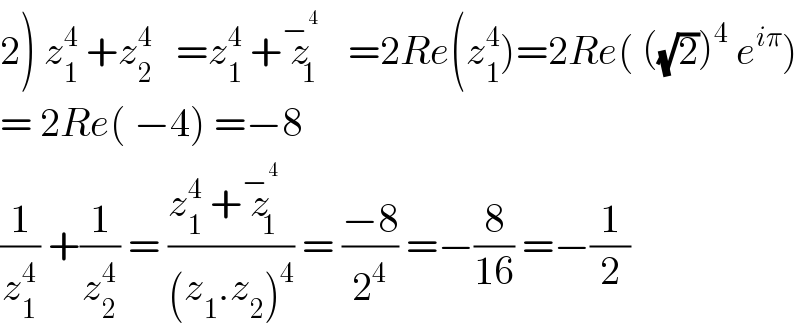
$$\left.\mathrm{2}\right)\:{z}_{\mathrm{1}} ^{\mathrm{4}} \:+{z}_{\mathrm{2}} ^{\mathrm{4}} \:\:\:={z}_{\mathrm{1}} ^{\mathrm{4}} \:+\overset{−^{\mathrm{4}} } {{z}}_{\mathrm{1}} \:\:=\mathrm{2}{Re}\left({z}_{\mathrm{1}} ^{\mathrm{4}} \right)=\mathrm{2}{Re}\left(\:\left(\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \:{e}^{{i}\pi} \right) \\ $$$$=\:\mathrm{2}{Re}\left(\:−\mathrm{4}\right)\:=−\mathrm{8} \\ $$$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{4}} }\:+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{4}} }\:=\:\frac{{z}_{\mathrm{1}} ^{\mathrm{4}} \:+\overset{−^{\mathrm{4}} } {{z}}_{\mathrm{1}} }{\left({z}_{\mathrm{1}} .{z}_{\mathrm{2}} \right)^{\mathrm{4}} }\:=\:\frac{−\mathrm{8}}{\mathrm{2}^{\mathrm{4}} }\:=−\frac{\mathrm{8}}{\mathrm{16}}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
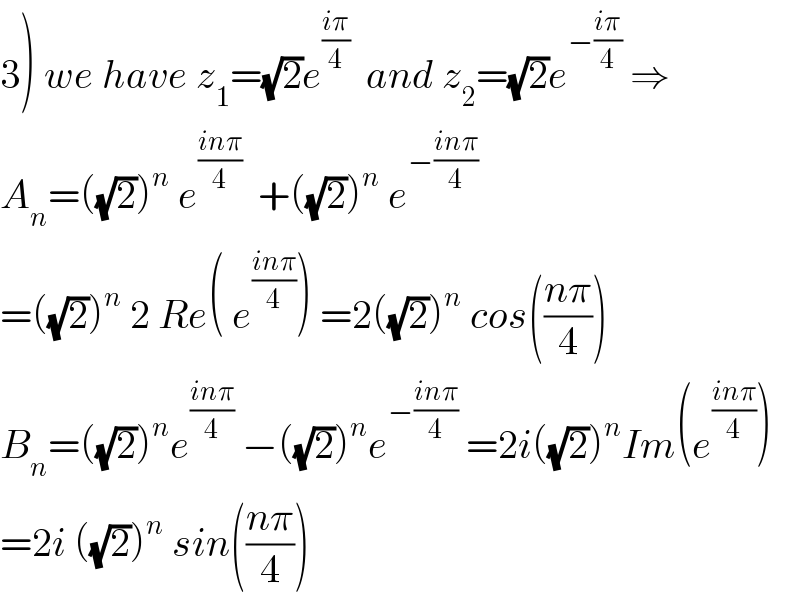
$$\left.\mathrm{3}\right)\:{we}\:{have}\:{z}_{\mathrm{1}} =\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:{and}\:{z}_{\mathrm{2}} =\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$${A}_{{n}} =\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} \:\:+\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{in}\pi}{\mathrm{4}}} \\ $$$$=\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\mathrm{2}\:{Re}\left(\:{e}^{\frac{{in}\pi}{\mathrm{4}}} \right)\:=\mathrm{2}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{cos}\left(\frac{{n}\pi}{\mathrm{4}}\right) \\ $$$${B}_{{n}} =\left(\sqrt{\mathrm{2}}\right)^{{n}} {e}^{\frac{{in}\pi}{\mathrm{4}}} \:−\left(\sqrt{\mathrm{2}}\right)^{{n}} {e}^{−\frac{{in}\pi}{\mathrm{4}}} \:=\mathrm{2}{i}\left(\sqrt{\mathrm{2}}\right)^{{n}} {Im}\left({e}^{\frac{{in}\pi}{\mathrm{4}}} \right) \\ $$$$=\mathrm{2}{i}\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right) \\ $$
Commented by math khazana by abdo last updated on 12/Aug/18
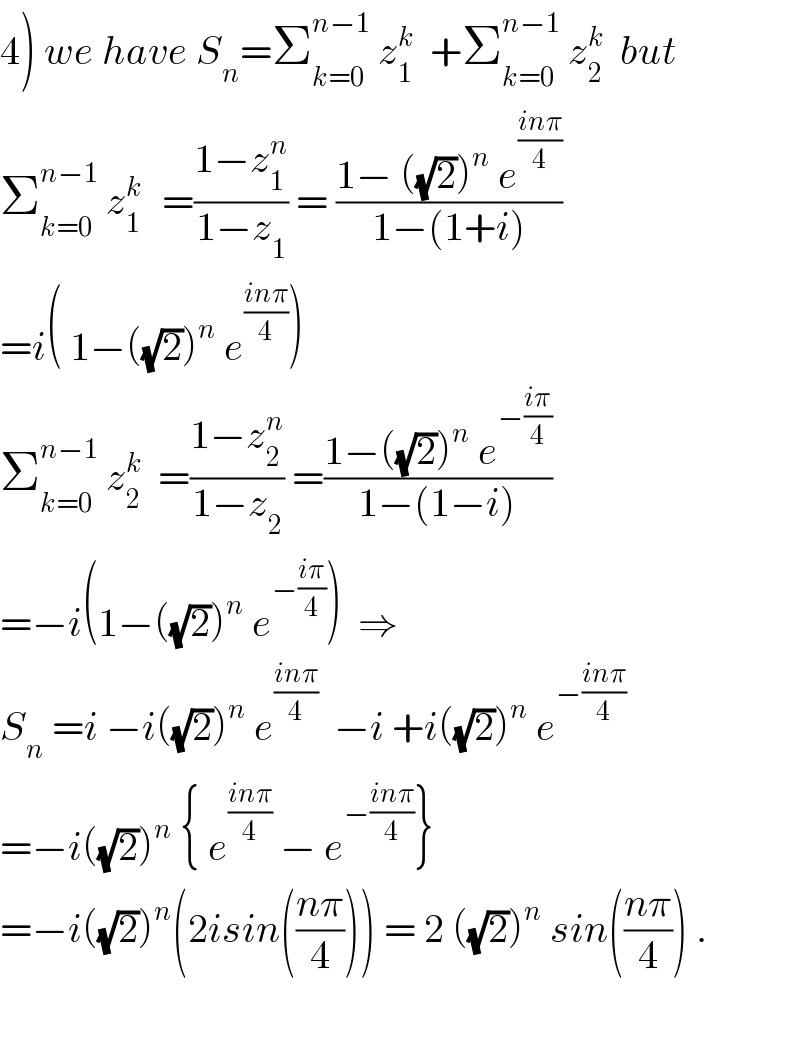
$$\left.\mathrm{4}\right)\:{we}\:{have}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{\mathrm{1}} ^{{k}} \:\:+\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{\mathrm{2}} ^{{k}} \:\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{\mathrm{1}} ^{{k}\:} \:\:=\frac{\mathrm{1}−{z}_{\mathrm{1}} ^{{n}} }{\mathrm{1}−{z}_{\mathrm{1}} }\:=\:\frac{\mathrm{1}−\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} }{\mathrm{1}−\left(\mathrm{1}+{i}\right)} \\ $$$$={i}\left(\:\mathrm{1}−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} \right) \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{z}_{\mathrm{2}} ^{{k}} \:\:=\frac{\mathrm{1}−{z}_{\mathrm{2}} ^{{n}} }{\mathrm{1}−{z}_{\mathrm{2}} }\:=\frac{\mathrm{1}−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{1}−\left(\mathrm{1}−{i}\right)} \\ $$$$=−{i}\left(\mathrm{1}−\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:\:\Rightarrow \\ $$$${S}_{{n}} \:={i}\:−{i}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{\frac{{in}\pi}{\mathrm{4}}} \:\:−{i}\:+{i}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{e}^{−\frac{{in}\pi}{\mathrm{4}}} \\ $$$$=−{i}\left(\sqrt{\mathrm{2}}\right)^{{n}} \:\left\{\:{e}^{\frac{{in}\pi}{\mathrm{4}}} \:−\:{e}^{−\frac{{in}\pi}{\mathrm{4}}} \right\} \\ $$$$=−{i}\left(\sqrt{\mathrm{2}}\right)^{{n}} \left(\mathrm{2}{isin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\right)\:=\:\mathrm{2}\:\left(\sqrt{\mathrm{2}}\right)^{{n}} \:{sin}\left(\frac{{n}\pi}{\mathrm{4}}\right)\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
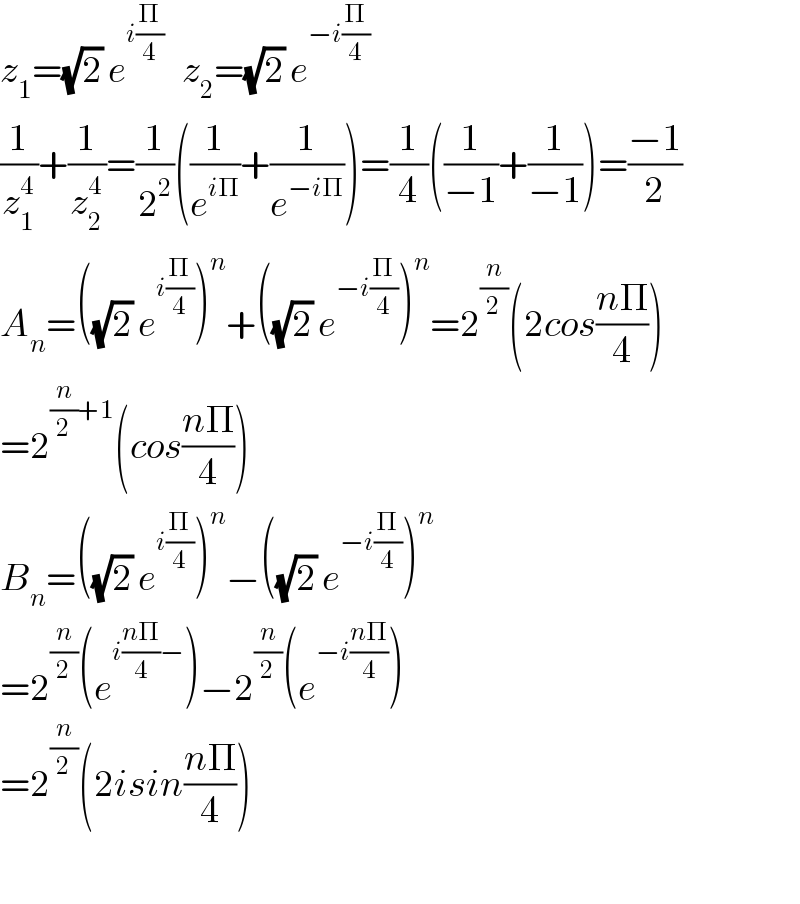
$${z}_{\mathrm{1}} =\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\Pi}{\mathrm{4}}} \:\:\:{z}_{\mathrm{2}} =\sqrt{\mathrm{2}}\:{e}^{−{i}\frac{\Pi}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{4}} }+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left(\frac{\mathrm{1}}{{e}^{{i}\Pi} }+\frac{\mathrm{1}}{{e}^{−{i}\Pi} }\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{−\mathrm{1}}+\frac{\mathrm{1}}{−\mathrm{1}}\right)=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$$${A}_{{n}} =\left(\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\Pi}{\mathrm{4}}} \right)^{{n}} +\left(\sqrt{\mathrm{2}}\:{e}^{−{i}\frac{\Pi}{\mathrm{4}}} \right)^{{n}} =\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \left(\mathrm{2}{cos}\frac{{n}\Pi}{\mathrm{4}}\right) \\ $$$$=\mathrm{2}^{\frac{{n}}{\mathrm{2}}+\mathrm{1}} \left({cos}\frac{{n}\Pi}{\mathrm{4}}\right) \\ $$$${B}_{{n}} =\left(\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\Pi}{\mathrm{4}}} \right)^{{n}} −\left(\sqrt{\mathrm{2}}\:{e}^{−{i}\frac{\Pi}{\mathrm{4}}} \right)^{{n}} \\ $$$$=\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \left({e}^{{i}\frac{{n}\Pi}{\mathrm{4}}−} \right)−\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \left({e}^{−{i}\frac{{n}\Pi}{\mathrm{4}}} \right) \\ $$$$=\mathrm{2}^{\frac{{n}}{\mathrm{2}}} \left(\mathrm{2}{isin}\frac{{n}\Pi}{\mathrm{4}}\right) \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
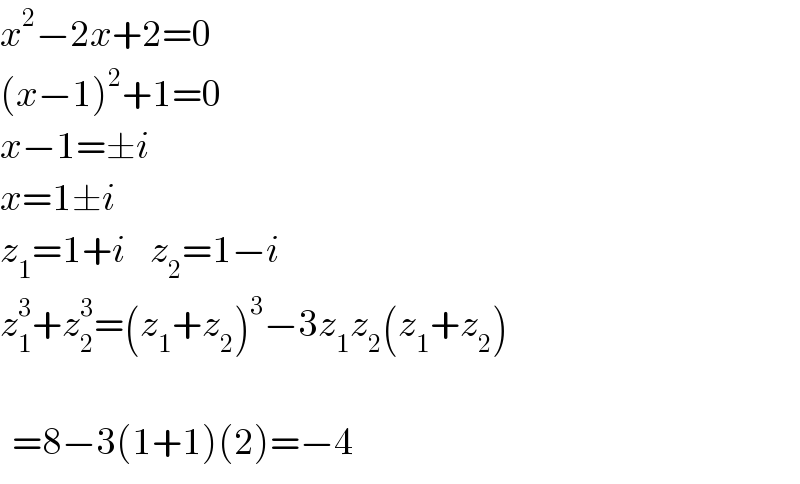
$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$${x}−\mathrm{1}=\pm{i} \\ $$$${x}=\mathrm{1}\pm{i} \\ $$$${z}_{\mathrm{1}} =\mathrm{1}+{i}\:\:\:\:{z}_{\mathrm{2}} =\mathrm{1}−{i} \\ $$$${z}_{\mathrm{1}} ^{\mathrm{3}} +{z}_{\mathrm{2}} ^{\mathrm{3}} =\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{z}_{\mathrm{1}} {z}_{\mathrm{2}} \left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right) \\ $$$$ \\ $$$$\:\:=\mathrm{8}−\mathrm{3}\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{2}\right)=−\mathrm{4} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
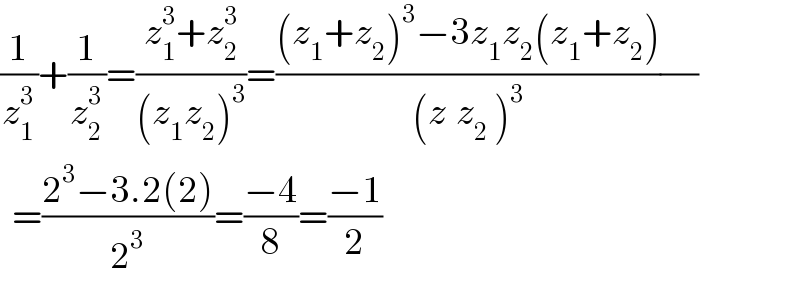
$$\frac{\mathrm{1}}{{z}_{\mathrm{1}} ^{\mathrm{3}} }+\frac{\mathrm{1}}{{z}_{\mathrm{2}} ^{\mathrm{3}} }=\frac{{z}_{\mathrm{1}} ^{\mathrm{3}} +{z}_{\mathrm{2}} ^{\mathrm{3}} }{\left({z}_{\mathrm{1}} {z}_{\mathrm{2}} \right)^{\mathrm{3}} }=\frac{\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{3}{z}_{\mathrm{1}} {z}_{\mathrm{2}} \left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)}{\left({z}_{} {z}_{\mathrm{2}} \:\right)^{\mathrm{3}} }\frac{}{} \\ $$$$\:\:=\frac{\mathrm{2}^{\mathrm{3}} −\mathrm{3}.\mathrm{2}\left(\mathrm{2}\right)}{\mathrm{2}^{\mathrm{3}} }=\frac{−\mathrm{4}}{\mathrm{8}}=\frac{−\mathrm{1}}{\mathrm{2}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
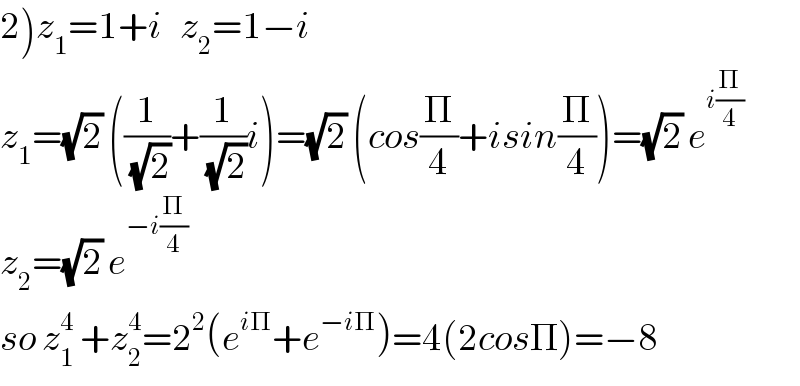
$$\left.\mathrm{2}\right){z}_{\mathrm{1}} =\mathrm{1}+{i}\:\:\:{z}_{\mathrm{2}} =\mathrm{1}−{i} \\ $$$${z}_{\mathrm{1}} =\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{i}\right)=\sqrt{\mathrm{2}}\:\left({cos}\frac{\Pi}{\mathrm{4}}+{isin}\frac{\Pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\Pi}{\mathrm{4}}} \\ $$$${z}_{\mathrm{2}} =\sqrt{\mathrm{2}}\:{e}^{−{i}\frac{\Pi}{\mathrm{4}}} \\ $$$${so}\:{z}_{\mathrm{1}} ^{\mathrm{4}} \:+{z}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{2}^{\mathrm{2}} \left({e}^{{i}\Pi} +{e}^{−{i}\Pi} \right)=\mathrm{4}\left(\mathrm{2}{cos}\Pi\right)=−\mathrm{8} \\ $$
