Menu Close

Question-41627

Tinku Tara 0 Comments
Pin




Question Number 41627 by alex041103 last updated on 10/Aug/18
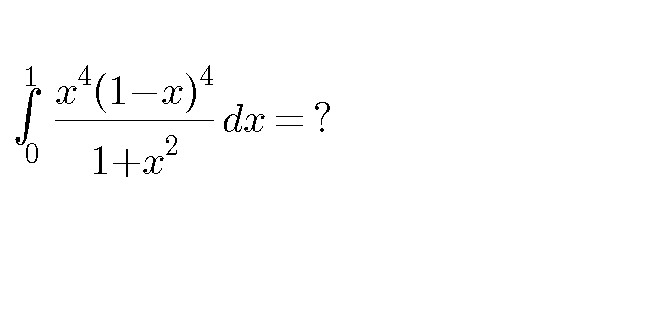
Commented by alex041103 last updated on 10/Aug/18
Just for fun! I have already posted this Q. around a year ago. The result is beautiful and worths giving it a try. Can you prove something interesting. Hint: Calculate the result.
$${Just}\:{for}\:{fun}!\:{I}\:{have}\:{already}\:{posted} \\ $$$${this}\:{Q}.\:{around}\:{a}\:{year}\:{ago}.\:{The}\:{result} \\ $$$${is}\:{beautiful}\:{and}\:{worths}\:{giving}\:{it}\:{a}\:{try}. \\ $$$${Can}\:{you}\:{prove}\:{something}\:{interesting}. \\ $$$${Hint}:\:{Calculate}\:{the}\:{result}. \\ $$
Commented by maxmathsup by imad last updated on 10/Aug/18
we have x^4 (1−x^ )^4 =x^4 (x^2 −2x+1)^2 =x^4 ( (x^2 −2x)^2 +2(x^2 −2x) +1) =x^4 { x^4 −4x^3 +4x^2 +2x^2 −4x +1} =x^4 { x^4 −4x^3 +6x^2 −4x+1} = x^8 −4x^7 +6x^6 −4x^5 +x^4 ⇒ I = ∫_0 ^1 ((x^8 −4x^7 +6x^6 −4x^5 +x^4 )/(1+x^2 )) dx = ∫_0 ^1 (x^8 −4x^7 +6x^6 −4x^5 +x^4 )Σ_(n=0) ^∞ (−1)^n x^(2n) dx = Σ_(n=0) ^∞ (−1)^(n ) ∫_0 ^1 (x^(2n+8) −x^(2n+7) +6 x^(2n+6) −4 x^(2n+5) +x^(2n+4) )dx = Σ_(n=0) ^∞ (((−1)^n )/(2n+9)) −Σ_(n=0) ^∞ (((−1)^n )/(2n+8)) +6 Σ_(n=0) ^∞ (((−1)^n )/(2n+7)) −4 Σ_(n=0) ^∞ (((−1)^n )/(2n+6)) +Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) let w(x) = Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) x^(2n+5) we have w(1) =Σ_(n=0) ^∞ (((−1)^n )/(2n+5)) w^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(2n+4) =x^4 Σ_(n=0) ^∞ (−x^2 )^n =(x^4 /(1+x^2 )) ⇒ w(x) = ∫_0 ^x (t^4 /(1+t^2 )) dt +c but c=w(0) =0 ⇒w(x)=∫_0 ^x (t^4 /(1+t^2 )) dt w(x)= ∫_0 ^x ((t^4 −1+1)/(t^2 +1)) dt = ∫_0 ^x (((t^2 +1)(t^2 −1) +1)/(t^2 +1)) dt =∫_0 ^x (t^2 −1)dt + ∫_0 ^x (dt/(1+t^2 )) = (x^3 /3) −x +arctan(x) ⇒ w(1) =−(2/3) +(π/4) generally let consider w_p (x) =Σ_(n=0) ^∞ (((−1)^n )/(2n+p)) x^(2n+p) we have w_p (1) =Σ_(n=0) ^∞ (((−1)^n )/(2n+p )) and we have w_p ^′ (x) = Σ_(n=0) ^∞ (−1)^n x^(2n+p−1) = x^(p−1) Σ_(n=0) ^∞ (−x^2 )^n = (x^(p−1) /(1+x^2 )) ⇒ w_p (x) = ∫_0 ^x (x^(p−1) /(1+x^2 )) dx +c but c=w_p (1)=0 ⇒w_p (x)= ∫_0 ^x (x^(p−1) /(1+x^2 )) dx ....be continued...
$${we}\:{have}\:{x}^{\mathrm{4}} \left(\mathrm{1}−{x}^{} \right)^{\mathrm{4}} \:={x}^{\mathrm{4}} \left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} \:={x}^{\mathrm{4}} \left(\:\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)^{\mathrm{2}} +\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{2}{x}\right)\:+\mathrm{1}\right) \\ $$$$={x}^{\mathrm{4}} \left\{\:{x}^{\mathrm{4}} \:−\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{4}{x}^{\mathrm{2}} \:+\mathrm{2}{x}^{\mathrm{2}} \:−\mathrm{4}{x}\:+\mathrm{1}\right\}\:={x}^{\mathrm{4}} \left\{\:{x}^{\mathrm{4}} \:−\mathrm{4}{x}^{\mathrm{3}} \:+\mathrm{6}{x}^{\mathrm{2}} \:−\mathrm{4}{x}+\mathrm{1}\right\} \\ $$$$=\:{x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} \:−\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} \:\Rightarrow \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} \:−\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\: \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{\mathrm{8}} \:−\mathrm{4}{x}^{\mathrm{7}} \:+\mathrm{6}{x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} \:+{x}^{\mathrm{4}} \right)\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}} \:{dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}\:\:} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\left({x}^{\mathrm{2}{n}+\mathrm{8}} \:−{x}^{\mathrm{2}{n}+\mathrm{7}} \:+\mathrm{6}\:{x}^{\mathrm{2}{n}+\mathrm{6}} \:−\mathrm{4}\:{x}^{\mathrm{2}{n}+\mathrm{5}} \:+{x}^{\mathrm{2}{n}+\mathrm{4}} \right){dx} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{9}}\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{8}}\:+\mathrm{6}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{7}}\:−\mathrm{4}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{6}}\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}} \\ $$$${let}\:\:{w}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}}\:{x}^{\mathrm{2}{n}+\mathrm{5}} \:\:{we}\:{have}\:{w}\left(\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{5}} \\ $$$${w}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{4}} \:={x}^{\mathrm{4}} \:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{t}^{\mathrm{4}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:+{c}\:\:{but}\:{c}={w}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow{w}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}^{\mathrm{4}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt} \\ $$$${w}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\frac{{t}^{\mathrm{4}} −\mathrm{1}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\:\int_{\mathrm{0}} ^{{x}} \:\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{1}\right)\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{{x}} \:\:\left({t}^{\mathrm{2}} −\mathrm{1}\right){dt}\:\:+\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\:−{x}\:\:+{arctan}\left({x}\right)\:\Rightarrow \\ $$$${w}\left(\mathrm{1}\right)\:=−\frac{\mathrm{2}}{\mathrm{3}}\:+\frac{\pi}{\mathrm{4}}\:\:{generally}\:{let}\:{consider}\:{w}_{{p}} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+{p}}\:{x}^{\mathrm{2}{n}+{p}} \\ $$$${we}\:{have}\:{w}_{{p}} \left(\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+{p}\:}\:\:\:{and}\:{we}\:{have} \\ $$$${w}_{{p}} ^{'} \left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}+{p}−\mathrm{1}} \:\:=\:{x}^{{p}−\mathrm{1}} \:\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${w}_{{p}} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:+{c}\:{but}\:{c}={w}_{{p}} \left(\mathrm{1}\right)=\mathrm{0}\:\Rightarrow{w}_{{p}} \left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\:\:\frac{{x}^{{p}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$….{be}\:{continued}… \\ $$$$ \\ $$
Answered by rahul 19 last updated on 10/Aug/18
Commented by rahul 19 last updated on 10/Aug/18
≠ 0 ����
Commented by alex041103 last updated on 10/Aug/18
Can you now prove, that ((22)/7)>π?
$${Can}\:{you}\:{now}\:{prove},\:{that}\:\frac{\mathrm{22}}{\mathrm{7}}>\pi? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 10/Aug/18
bah darun excellent...
$${bah}\:{darun}\:{excellent}… \\ $$
Commented by rahul 19 last updated on 10/Aug/18
Since integrand is non−negative & continous everywhere, it must be strictly positive in [0,1]. 0< ((22)/7)−π ⇒ ((22)/7)>π.
$$\mathrm{Since}\:\mathrm{integrand}\:\mathrm{is}\:\mathrm{non}−\mathrm{negative}\:\& \\ $$$$\mathrm{continous}\:\mathrm{everywhere},\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\mathrm{strictly} \\ $$$$\mathrm{positive}\:\mathrm{in}\:\left[\mathrm{0},\mathrm{1}\right]. \\ $$$$\mathrm{0}<\:\frac{\mathrm{22}}{\mathrm{7}}−\pi\: \\ $$$$\Rightarrow\:\frac{\mathrm{22}}{\mathrm{7}}>\pi. \\ $$
Commented by alex041103 last updated on 10/Aug/18
Exactly. Also you can see thatfor 0<x<1 the integrand is small... this implies that ((22)/7) is good rational approximation for π.
$${Exactly}. \\ $$$${Also}\:{you}\:{can}\:{see}\:{thatfor}\:\mathrm{0}<{x}<\mathrm{1}\:{the} \\ $$$${integrand}\:{is}\:{small}…\:{this}\:{implies}\:{that} \\ $$$$\frac{\mathrm{22}}{\mathrm{7}}\:{is}\:\:{good}\:{rational}\:{approximation} \\ $$$${for}\:\pi. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *