Question Number 172732 by depressiveshrek last updated on 30/Jun/22
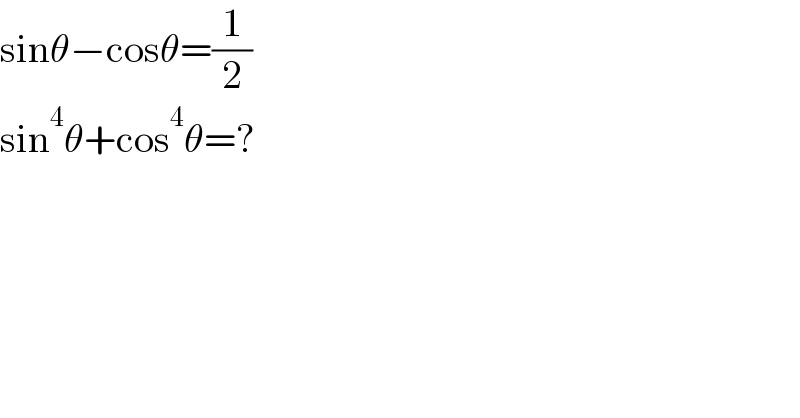
$$\mathrm{sin}\theta−\mathrm{cos}\theta=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta=? \\ $$
Answered by floor(10²Eta[1]) last updated on 30/Jun/22
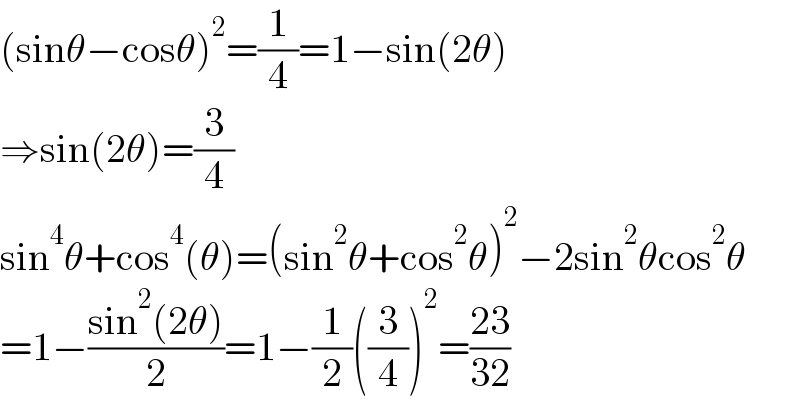
$$\left(\mathrm{sin}\theta−\mathrm{cos}\theta\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{1}−\mathrm{sin}\left(\mathrm{2}\theta\right) \\ $$$$\Rightarrow\mathrm{sin}\left(\mathrm{2}\theta\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \left(\theta\right)=\left(\mathrm{sin}^{\mathrm{2}} \theta+\mathrm{cos}^{\mathrm{2}} \theta\right)^{\mathrm{2}} −\mathrm{2sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta \\ $$$$=\mathrm{1}−\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right)}{\mathrm{2}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{23}}{\mathrm{32}} \\ $$
Answered by uochiton last updated on 01/Jul/22
![(sin θ − cos θ)^4 =(1/(16)) sin^4 θ−4∙sin^3 θ∙cos θ +6∙sin^2 θ ∙ cos^2 θ −4∙sin θ∙cos^3 +cos^4 θ=(1/(16)) sin^4 θ+cos^4 θ−2∙sin θ∙cos θ∙(2∙sin^2 θ −3∙sin θ∙cos θ+2∙cos^2 θ)=(1/(16)) sin^4 θ+cos^4 θ−sin 2∙θ ∙(2−3∙sin θ∙cos θ)=(1/(16)) sin^4 θ+cos^4 θ −sin 2∙θ ∙[2−(3/2)∙( 2∙sin θ ∙cos θ)]=(1/(16)) sin^4 θ+cos^4 θ−sin 2∙θ ∙(2−(3/2)∙sin 2∙θ)=(1/(16)) sin^4 θ+cos^4 θ−(3/4)∙(2− (3/2)∙(3/4))=(1/(16)) sin^4 θ+cos^4 θ−(3/4)∙(2−(9/8))=(1/(16)) sin^4 θ+cos^4 θ−(3/4)∙((7/8))=(1/(16)) sin^4 θ+cos^4 θ−((21)/(32))=(1/(16)) sin^4 θ+cos^4 θ=((23)/(32)) (sin θ−cos θ)^2 =(1/4) sin^2 θ−2∙sin θ∙cos θ+cos^2 θ =(1/4) 1−sin 2∙θ=(1/4) sin 2∙θ=(3/4) 1 11 121 1331 14641](https://www.tinkutara.com/question/Q172752.png)
$$ \\ $$$$\left(\mathrm{sin}\:\theta\:−\:\mathrm{cos}\:\theta\right)^{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:\theta−\mathrm{4}\centerdot\mathrm{sin}^{\mathrm{3}} \theta\centerdot\mathrm{cos}\:\theta\:+\mathrm{6}\centerdot\mathrm{sin}^{\mathrm{2}} \:\theta\:\centerdot\:\mathrm{cos}^{\mathrm{2}} \theta\:−\mathrm{4}\centerdot\mathrm{sin}\:\theta\centerdot\mathrm{cos}^{\mathrm{3}} +\mathrm{cos}^{\mathrm{4}} \theta=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{2}\centerdot\mathrm{sin}\:\theta\centerdot\mathrm{cos}\:\theta\centerdot\left(\mathrm{2}\centerdot\mathrm{sin}^{\mathrm{2}} \theta\:−\mathrm{3}\centerdot\mathrm{sin}\:\theta\centerdot\mathrm{cos}\:\theta+\mathrm{2}\centerdot\mathrm{cos}^{\mathrm{2}} \theta\right)=\frac{\mathrm{1}}{\mathrm{16}}\:\:\:\: \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{sin}\:\mathrm{2}\centerdot\theta\:\centerdot\left(\mathrm{2}−\mathrm{3}\centerdot\mathrm{sin}\:\theta\centerdot\mathrm{cos}\:\theta\right)=\frac{\mathrm{1}}{\mathrm{16}}\:\: \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta\:−\mathrm{sin}\:\mathrm{2}\centerdot\theta\:\centerdot\left[\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}\centerdot\left(\:\mathrm{2}\centerdot\mathrm{sin}\:\theta\:\centerdot\mathrm{cos}\:\theta\right)\right]=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\mathrm{sin}\:\mathrm{2}\centerdot\theta\:\centerdot\left(\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}\centerdot\mathrm{sin}\:\mathrm{2}\centerdot\theta\right)=\frac{\mathrm{1}}{\mathrm{16}}\:\: \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\frac{\mathrm{3}}{\mathrm{4}}\centerdot\left(\mathrm{2}−\:\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{3}}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\frac{\mathrm{3}}{\mathrm{4}}\centerdot\left(\mathrm{2}−\frac{\mathrm{9}}{\mathrm{8}}\right)=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\frac{\mathrm{3}}{\mathrm{4}}\centerdot\left(\frac{\mathrm{7}}{\mathrm{8}}\right)=\frac{\mathrm{1}}{\mathrm{16}}\:\:\:\: \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta−\frac{\mathrm{21}}{\mathrm{32}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\mathrm{sin}^{\mathrm{4}} \theta+\mathrm{cos}^{\mathrm{4}} \theta=\frac{\mathrm{23}}{\mathrm{32}} \\ $$$$\:\: \\ $$$$ \\ $$$$\left(\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \theta−\mathrm{2}\centerdot\mathrm{sin}\:\theta\centerdot\mathrm{cos}\:\theta+\mathrm{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{1}−\mathrm{sin}\:\mathrm{2}\centerdot\theta=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{2}\centerdot\theta=\frac{\mathrm{3}}{\mathrm{4}}\: \\ $$$$\mathrm{1} \\ $$$$\mathrm{11} \\ $$$$\mathrm{121} \\ $$$$\mathrm{1331} \\ $$$$\mathrm{14641} \\ $$
