bemath-lim-x-2-x-3-x-1-x-

Question Number 107207 by bemath last updated on 09/Aug/20

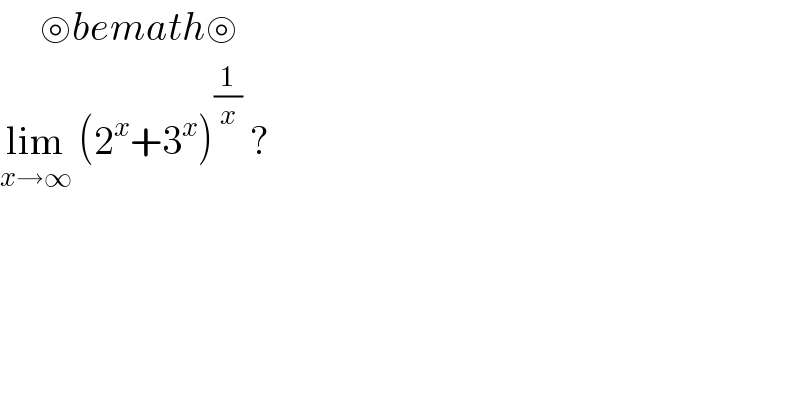
$$\:\:\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\frac{\mathrm{1}}{{x}}} \:?\: \\ $$

Answered by Dwaipayan Shikari last updated on 09/Aug/20

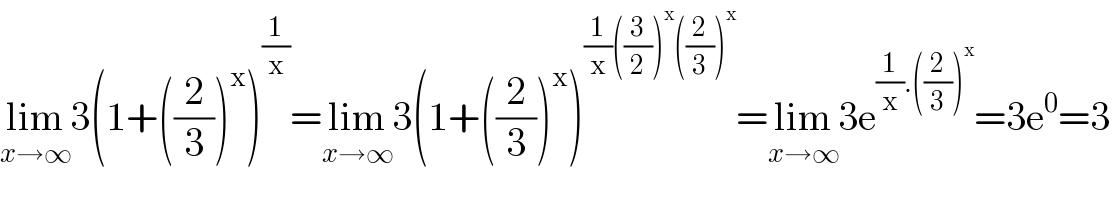
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}3}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}3}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right)^{\frac{\mathrm{1}}{\mathrm{x}}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{x}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} } =\underset{{x}\rightarrow\infty} {\mathrm{lim}3e}^{\frac{\mathrm{1}}{\mathrm{x}}.\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} } =\mathrm{3e}^{\mathrm{0}} =\mathrm{3} \\ $$

Answered by bemath last updated on 09/Aug/20

Answered by Dwaipayan Shikari last updated on 09/Aug/20

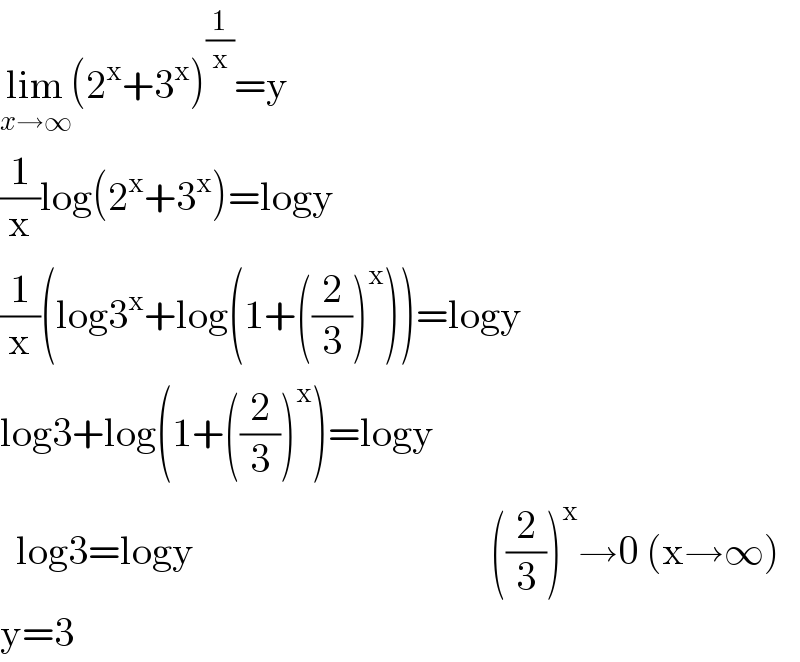
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{2}^{\mathrm{x}} +\mathrm{3}^{\mathrm{x}} \right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\mathrm{y} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\mathrm{log}\left(\mathrm{2}^{\mathrm{x}} +\mathrm{3}^{\mathrm{x}} \right)=\mathrm{logy} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\left(\mathrm{log3}^{\mathrm{x}} +\mathrm{log}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right)\right)=\mathrm{logy} \\ $$$$\mathrm{log3}+\mathrm{log}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right)=\mathrm{logy} \\ $$$$\:\:\mathrm{log3}=\mathrm{logy}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \rightarrow\mathrm{0}\:\left(\mathrm{x}\rightarrow\infty\right) \\ $$$$\mathrm{y}=\mathrm{3} \\ $$

Answered by 1549442205PVT last updated on 10/Aug/20

$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}\:}\left(\mathrm{2}^{{x}} +\mathrm{3}^{{x}} \right)^{\frac{\mathrm{1}}{{x}}} \:=\mathrm{lim}\left[\mathrm{3}^{\mathrm{x}} \left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right]^{\frac{\mathrm{1}}{\mathrm{x}}} \right. \\ $$$$=\mathrm{l}\underset{\mathrm{x}\rightarrow\infty} {\mathrm{im}\:}\mathrm{3}.\left[\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right]^{\frac{\mathrm{1}}{\mathrm{x}}} =\right. \\ $$$$\mathrm{3}.\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{x}} \right]^{\frac{\mathrm{1}}{\mathrm{x}}} =\mathrm{3}.\left[\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\infty} \right]^{\frac{\mathrm{1}}{\infty}} \right. \\ $$$$=\mathrm{3}.\left(\mathrm{1}+\mathrm{0}\right)^{\mathrm{0}} =\mathrm{3}.\mathrm{1}=\mathrm{3} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com