Question Number 107318 by bemath last updated on 10/Aug/20
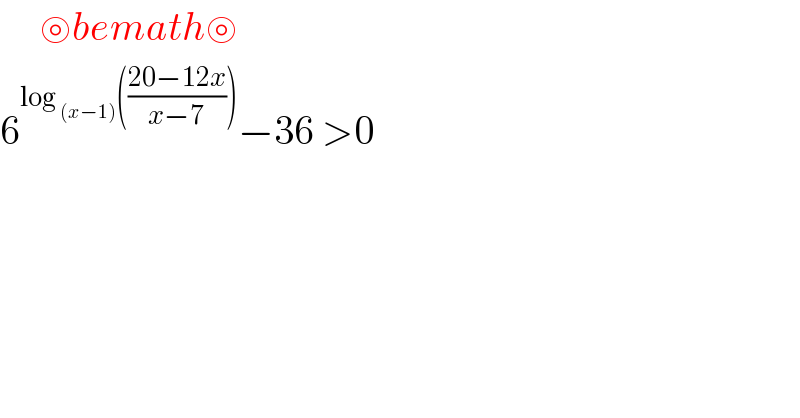
$$\:\:\:\:\:\circledcirc{bemath}\circledcirc \\ $$$$\mathrm{6}^{\mathrm{log}\:_{\left({x}−\mathrm{1}\right)} \left(\frac{\mathrm{20}−\mathrm{12}{x}}{{x}−\mathrm{7}}\right)} −\mathrm{36}\:>\mathrm{0} \\ $$
Answered by bobhans last updated on 10/Aug/20

$$\:\:\:\:\:\:\:\:\:\circledast\mathcal{BOBHANS}\circledast \\ $$$$\Rightarrow\:\mathrm{6}^{\mathrm{log}\:_{\left(\mathrm{x}−\mathrm{1}\right)} \left(\frac{\mathrm{20}−\mathrm{12x}}{\mathrm{x}−\mathrm{7}}\right)} \:>\:\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{log}\:_{\left(\mathrm{x}−\mathrm{1}\right)} \left(\frac{\mathrm{20}−\mathrm{12x}}{\mathrm{x}−\mathrm{7}}\right)\:>\:\mathrm{log}\:_{\left(\mathrm{x}−\mathrm{1}\right)} \left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\begin{cases}{\frac{\mathrm{20}−\mathrm{12x}}{\mathrm{x}−\mathrm{7}}\:>\:\mathrm{0}\:\Rightarrow\frac{\mathrm{12x}−\mathrm{20}}{\mathrm{x}−\mathrm{7}}\:<\mathrm{0}\:\Rightarrow\frac{\mathrm{5}}{\mathrm{3}}\:<\:\mathrm{x}\:<\:\mathrm{7}}\\{\left(\mathrm{x}−\mathrm{1}−\mathrm{1}\right)\left(\frac{\mathrm{20}−\mathrm{12x}}{\mathrm{x}−\mathrm{7}}−\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{1}\right)\:>\:\mathrm{0}}\end{cases} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)\left(\frac{−\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{3}} }{\mathrm{x}−\mathrm{7}}\right)\:>\:\mathrm{0}\:\Rightarrow\frac{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{3}} }{\mathrm{x}−\mathrm{7}}\:<\mathrm{0} \\ $$$$\mathrm{x}<\mathrm{2}\:\cup\:\mathrm{3}<\:\mathrm{x}\:<\:\mathrm{7} \\ $$$$\mathrm{the}\:\mathrm{solution}\:\mathrm{is}\:\left(\mathrm{1}\right)\cap\left(\mathrm{2}\right) \\ $$$$\mathrm{x}\:\in\:\left(\mathrm{3},\:\mathrm{7}\right)\:\mathrm{or}\:\mathrm{3}\:<\:\mathrm{x}\:<\:\mathrm{7}\: \\ $$
