Question Number 173062 by Gbenga last updated on 06/Jul/22

Commented by kaivan.ahmadi last updated on 06/Jul/22
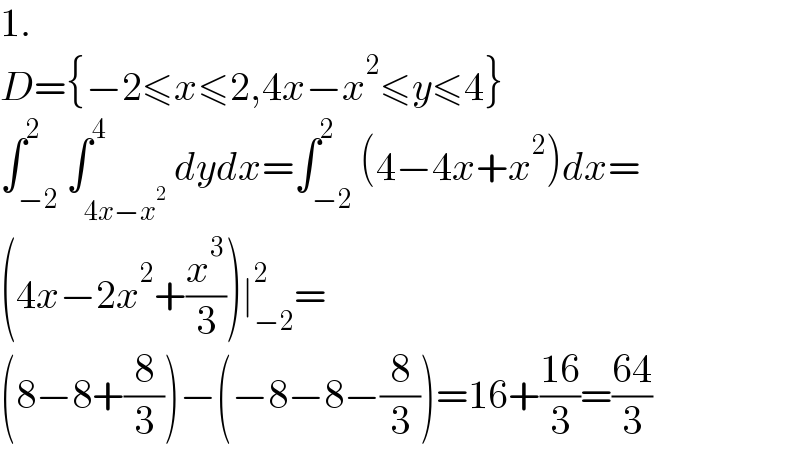
$$\mathrm{1}. \\ $$$${D}=\left\{−\mathrm{2}\leqslant{x}\leqslant\mathrm{2},\mathrm{4}{x}−{x}^{\mathrm{2}} \leqslant{y}\leqslant\mathrm{4}\right\} \\ $$$$\int_{−\mathrm{2}} ^{\mathrm{2}} \int_{\mathrm{4}{x}−{x}^{\mathrm{2}} } ^{\mathrm{4}} {dydx}=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{4}−\mathrm{4}{x}+{x}^{\mathrm{2}} \right){dx}= \\ $$$$\left(\mathrm{4}{x}−\mathrm{2}{x}^{\mathrm{2}} +\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right)\mid_{−\mathrm{2}} ^{\mathrm{2}} = \\ $$$$\left(\mathrm{8}−\mathrm{8}+\frac{\mathrm{8}}{\mathrm{3}}\right)−\left(−\mathrm{8}−\mathrm{8}−\frac{\mathrm{8}}{\mathrm{3}}\right)=\mathrm{16}+\frac{\mathrm{16}}{\mathrm{3}}=\frac{\mathrm{64}}{\mathrm{3}} \\ $$
Commented by Gbenga last updated on 06/Jul/22

$$\boldsymbol{\mathrm{great}}\:\boldsymbol{\mathrm{work}}\:\boldsymbol{\mathrm{sir}} \\ $$
