Menu Close

L-lim-x-0-2-x-1-1-2-1-x-

Tinku Tara 0 Comments
Pin




Question Number 107550 by ajfour last updated on 11/Aug/20
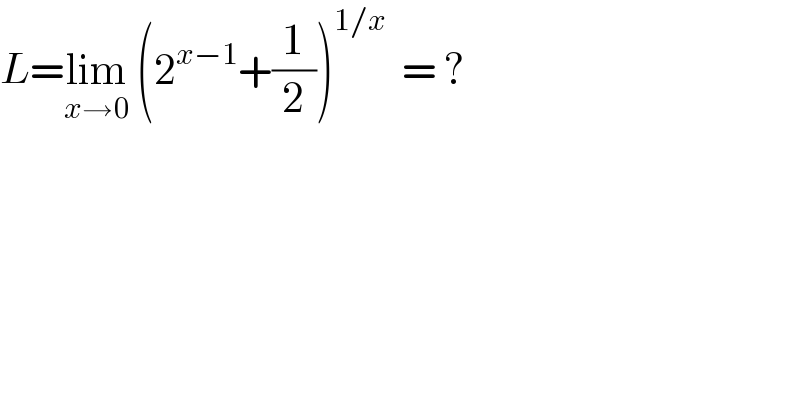
L=lim_(x→0) (2^(x−1) +(1/2))^(1/x) = ?
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{2}^{{x}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{1}/{x}} \:\:=\:? \\ $$
Answered by hgrocks last updated on 11/Aug/20
Commented by ajfour last updated on 11/Aug/20
Good, thanks Sir.
$${Good},\:{thanks}\:{Sir}. \\ $$
Answered by john santu last updated on 11/Aug/20
⋇JS⋇ L = lim_(x→0) ((1/2).2^x +(1/2))^(1/x) L=lim_(x→0) (2^(x−1) (1+(1/2^x )))^(1/x) ln L=lim_(x→0) ((ln (2^(x−1) )+ln (1+2^(−x) ))/x) ln L=lim_(x→0) ((2^(x−1) ln (2))/2^(x−1) )−((2^(−x) ln (2))/(1+2^(−x) )) ln L=(((1/2)ln (2))/(1/2))−((ln (2))/2) = (1/2)ln (2)=ln ((√2)) L= (√2)
$$\:\:\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\mathcal{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}^{{x}} +\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathcal{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{2}^{{x}−\mathrm{1}} \:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{{x}} }\right)\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{ln}\:\mathcal{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\:\left(\mathrm{2}^{{x}−\mathrm{1}} \right)+\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2}^{−{x}} \right)}{{x}} \\ $$$$\mathrm{ln}\:\mathcal{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{{x}−\mathrm{1}} \:\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{2}^{{x}−\mathrm{1}} }−\frac{\mathrm{2}^{−{x}} \:\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{1}+\mathrm{2}^{−{x}} } \\ $$$$\mathrm{ln}\:\mathcal{L}=\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}\right)}{\frac{\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{ln}\:\left(\mathrm{2}\right)}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}\right)=\mathrm{ln}\:\left(\sqrt{\mathrm{2}}\right) \\ $$$$\mathcal{L}=\:\sqrt{\mathrm{2}} \\ $$
Commented by ajfour last updated on 11/Aug/20
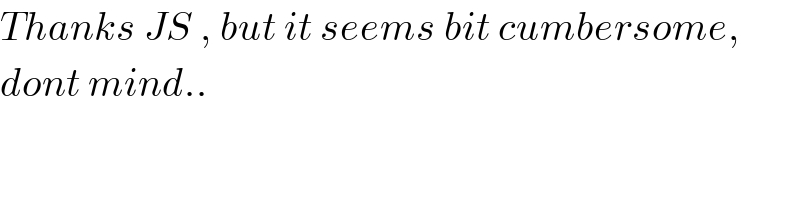
Thanks JS , but it seems bit cumbersome, dont mind..
$${Thanks}\:{JS}\:,\:{but}\:{it}\:{seems}\:{bit}\:{cumbersome}, \\ $$$${dont}\:{mind}.. \\ $$
Commented by john santu last updated on 11/Aug/20
no problem. up to you
Answered by Dwaipayan Shikari last updated on 11/Aug/20
lim_(x→0) (1/x)log(1+2^(x−1) −(1/2))=logy (1/x).(2^(x−1) −(1/2))=logy (1/2).((2^x −1)/x)=logy ((log(2))/2)=logy y=(√2)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}{log}\left(\mathrm{1}+\mathrm{2}^{{x}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\right)={logy} \\ $$$$\frac{\mathrm{1}}{{x}}.\left(\mathrm{2}^{{x}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\right)={logy} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}^{{x}} −\mathrm{1}}{{x}}={logy} \\ $$$$\frac{{log}\left(\mathrm{2}\right)}{\mathrm{2}}={logy} \\ $$$${y}=\sqrt{\mathrm{2}} \\ $$
Commented by ajfour last updated on 11/Aug/20
Quite nice, thanks!
$${Quite}\:{nice},\:{thanks}! \\ $$
Answered by ajfour last updated on 11/Aug/20
L=lim_(x→0) (1+((2^x −1)/x).(x/2))^(1/x) = lim_(x→0) {(1+(x/2)ln 2)^(2/(xln 2)) }^((ln 2)/2) L =e^(ln (√2)) = (√2) .
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{2}^{{x}} −\mathrm{1}}{{x}}.\frac{{x}}{\mathrm{2}}\right)^{\mathrm{1}/{x}} \\ $$$$\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\mathrm{ln}\:\mathrm{2}\right)^{\frac{\mathrm{2}}{{x}\mathrm{ln}\:\mathrm{2}}} \right\}^{\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}} \\ $$$$\:{L}\:={e}^{\mathrm{ln}\:\sqrt{\mathrm{2}}} \:=\:\sqrt{\mathrm{2}}\:. \\ $$
Answered by mathmax by abdo last updated on 11/Aug/20
f(x)=(2^(x−1) +(1/2))^(1/x) ⇒f(x) =e^((1/x)ln(2^(x−1) +(1/2))) we have 2^(x−1) =e^((x−1)ln(2)) =e^(−ln(2)) .e^(xln(2) ) ∼e^(−ln(2)) {1+xln(2)}=(1/2)(1+xln(2)) ⇒2^(x−1) +(1/2)∼1+x((ln(2))/2) ⇒ln(2^(x−1) +(1/2))∼ln(1+xln(2))∼(x/2)ln(2) ⇒ (1/x)ln(2^(x−1) +(1/2))∼(1/2)ln(2) =ln((√2)) ⇒lim_(x→0^+ ) f(x) =(√2)
$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)} \mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:=\mathrm{e}^{\left(\mathrm{x}−\mathrm{1}\right)\mathrm{ln}\left(\mathrm{2}\right)} \:=\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2}\right)} .\mathrm{e}^{\mathrm{xln}\left(\mathrm{2}\right)\:} \sim\mathrm{e}^{−\mathrm{ln}\left(\mathrm{2}\right)} \left\{\mathrm{1}+\mathrm{xln}\left(\mathrm{2}\right)\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{xln}\left(\mathrm{2}\right)\right) \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\sim\mathrm{1}+\mathrm{x}\frac{\mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\Rightarrow\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)\sim\mathrm{ln}\left(\mathrm{1}+\mathrm{xln}\left(\mathrm{2}\right)\right)\sim\frac{\mathrm{x}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\mathrm{2}^{\mathrm{x}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{2}}\right)\sim\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:=\mathrm{ln}\left(\sqrt{\mathrm{2}}\right)\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *