Question-107673

Question Number 107673 by qwerty111 last updated on 12/Aug/20

Answered by Her_Majesty last updated on 12/Aug/20

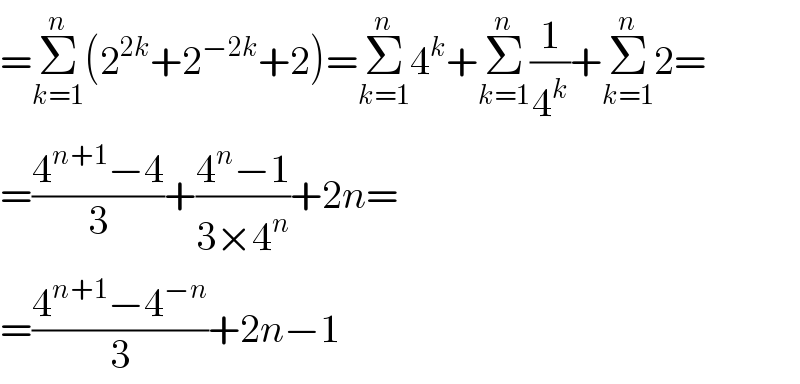
=Σ_(k=1) ^n (2^(2k) +2^(−2k) +2)=Σ_(k=1) ^n 4^k +Σ_(k=1) ^n (1/4^k )+Σ_(k=1) ^n 2= =((4^(n+1) −4)/3)+((4^n −1)/(3×4^n ))+2n= =((4^(n+1) −4^(−n) )/3)+2n−1

$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{2}^{\mathrm{2}{k}} +\mathrm{2}^{−\mathrm{2}{k}} +\mathrm{2}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{4}^{{k}} +\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{k}} }+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{2}= \\ $$$$=\frac{\mathrm{4}^{{n}+\mathrm{1}} −\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{4}^{{n}} −\mathrm{1}}{\mathrm{3}×\mathrm{4}^{{n}} }+\mathrm{2}{n}= \\ $$$$=\frac{\mathrm{4}^{{n}+\mathrm{1}} −\mathrm{4}^{−{n}} }{\mathrm{3}}+\mathrm{2}{n}−\mathrm{1} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Aug/20

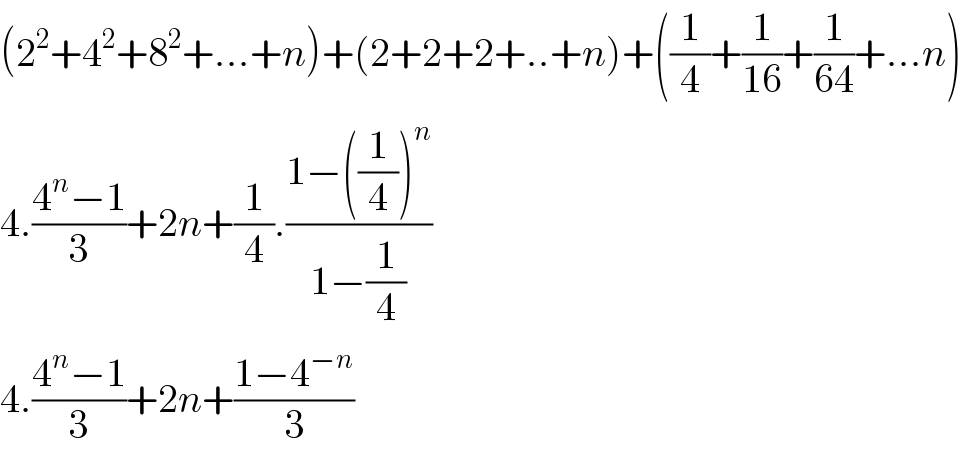
(2^2 +4^2 +8^2 +...+n)+(2+2+2+..+n)+((1/4)+(1/(16))+(1/(64))+...n) 4.((4^n −1)/3)+2n+(1/4).((1−((1/4))^n )/(1−(1/4))) 4.((4^n −1)/3)+2n+((1−4^(−n) )/3)

$$\left(\mathrm{2}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} +…+{n}\right)+\left(\mathrm{2}+\mathrm{2}+\mathrm{2}+..+{n}\right)+\left(\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{64}}+…{n}\right) \\ $$$$\mathrm{4}.\frac{\mathrm{4}^{{n}} −\mathrm{1}}{\mathrm{3}}+\mathrm{2}{n}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{n}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\mathrm{4}.\frac{\mathrm{4}^{{n}} −\mathrm{1}}{\mathrm{3}}+\mathrm{2}{n}+\frac{\mathrm{1}−\mathrm{4}^{−{n}} }{\mathrm{3}} \\ $$

Commented by Her_Majesty last updated on 12/Aug/20

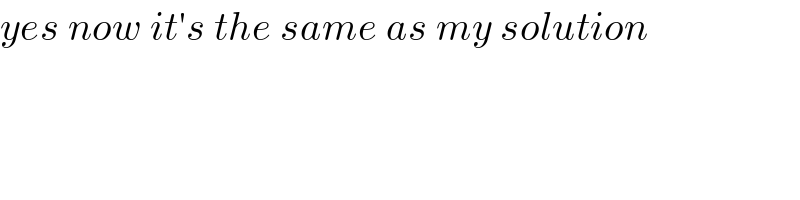
$${yes}\:{now}\:{it}'{s}\:{the}\:{same}\:{as}\:{my}\:{solution} \\ $$

Answered by 1549442205PVT last updated on 12/Aug/20

(2^n +(1/2^n ))^2 =4^n +2+(1/4^n ).Therefore, Σ_(k=1) ^n (2^n +(1/2^n ))^2 =2n+Σ_(k=1) ^(n) 4^n +Σ_(k=1) ^(n) (1/4^n ) =4.((4^n −1)/(4−1))+(1/4).((1−((1/4))^n )/(1−(1/4)))=2n+(4/3)(4^n −1) +(1/3)[1−((1/4))^n ]=2n−1+(4^(n+1) /3)−(1/(3.4^( n) ))

$$\left(\mathrm{2}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\right)^{\mathrm{2}} =\mathrm{4}^{\mathrm{n}} +\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{n}} }.\mathrm{Therefore}, \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\mathrm{2}^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\right)^{\mathrm{2}} =\mathrm{2n}+\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\mathrm{4}^{\mathrm{n}} +\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\Sigma}}\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{n}} } \\ $$$$=\mathrm{4}.\frac{\mathrm{4}^{\mathrm{n}} −\mathrm{1}}{\mathrm{4}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{n}} }{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{2n}+\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{4}^{\mathrm{n}} −\mathrm{1}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\boldsymbol{\mathrm{n}}} \right]=\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}+\frac{\mathrm{4}^{\boldsymbol{\mathrm{n}}+\mathrm{1}} }{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}.\mathrm{4}^{\:\boldsymbol{\mathrm{n}}} } \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply