Question Number 42190 by maxmathsup by imad last updated on 19/Aug/18
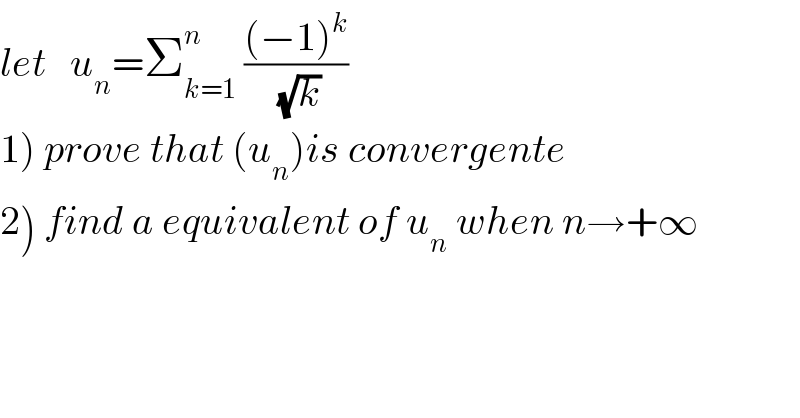
$${let}\:\:\:{u}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{\:\sqrt{{k}}} \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\left({u}_{{n}} \right){is}\:{convergente} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{equivalent}\:{of}\:{u}_{{n}} \:{when}\:{n}\rightarrow+\infty \\ $$
Commented by maxmathsup by imad last updated on 21/Aug/18
![1) we have lim_(n→+∞) u_n = Σ_(k=1) ^∞ (((−1)^k )/( (√k))) and this serie is convergente (alternate serie) 2) we have u_n =Σ_(p=1) ^([(n/2)]) (1/( (√(2p)))) −Σ_(p=0) ^([((n−1)/2)]) (1/( (√(2p+1)))) = Σ v_p −Σw_p (v_p )is decreasing ⇒ ∫_p ^(p+1) (dx/( (√(2x)))) ≤ v_p ≤ ∫_(p−1) ^p (dx/( (√(2x)))) ⇒ Σ_(p=1) ^([(n/2)]) ∫_p ^(p+1) (dx/( (√(2x)))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ Σ_(p=1) ^([(n/2)]) ∫_(p−1) ^p (dx/( (√(2x)))) ⇒ ∫_1 ^([(n/2)] +1) (dx/( (√(2x)))) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤ ∫_0 ^([(n/2)]) (dx/( (√(2x)))) ⇒ (1/( (√2)))[2(√x)]_1 ^([(n/2)]+1) ≤ Σ_(p=1) ^([(n/2)]) v_p ≤(1/( (√2)))[2(√x)]_0 ^([(n/2)]) ⇒ (√2){(√([(n/2)]+1))−1}≤Σ v_p ≤(√2)(√([(n/2)])) also (w_p ) is decreasing ⇒ ∫_p ^(p+1) (dx/( (√(2x+1)))) ≤ w_p ≤ ∫_(p−1) ^p (dx/( (√(2x+1)))) ⇒ Σ_(p=1) ^([((n−1)/2)]) ∫_p ^(p+1) (dx/( (√(2x+1)))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ Σ_(p=1) ^([((n−1)/2)]) ∫_(p−1) ^p (dx/( (√(2x+1)))) ⇒ ∫_1 ^([((n−1)/2)] +1) (dx/( (√(2x+1)))) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ ∫_0 ^([((n−1)/2)]) (dx/( (√(2x +1)))) ⇒ [(√(2x+1))]_1 ^((([n−1)/2)]+1) ≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤ [(√(2x+1))]_0 ^([((n−1)/2)]) ⇒ (√(2[((n−1)/2)]+2)) −(√3)≤ Σ_(p=1) ^([((n−1)/2)]) w_p ≤(√(2[((n−1)/2)]+1))−1 ⇒ (√(2[((n−1)/2)]+2))+1−(√3)≤ Σ_(p=0) ^([((n−1)/2)]) w_p ≤ (√(2[((n−1)/2)]+1)) −2 ⇒ (√2){(√([(n/2)]+1))−1} +2−(√(2[((n−1)/2)]+1))≤ u_n ≤ (√2)(√([(n/2)])) +(√3)−1−(√(2[((n−1)/2)]+1)) ...be continued ...](https://www.tinkutara.com/question/Q42270.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \:=\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{\:\sqrt{{k}}}\:\:\:\:\:{and}\:{this}\:{serie}\:{is}\:{convergente} \\ $$$$\left({alternate}\:{serie}\right) \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{u}_{{n}} =\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{p}}}\:−\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{p}+\mathrm{1}}}\:=\:\Sigma\:{v}_{{p}} \:−\Sigma{w}_{{p}} \\ $$$$\left({v}_{{p}} \right){is}\:{decreasing}\:\Rightarrow\:\int_{{p}} ^{{p}+\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\leqslant\:{v}_{{p}} \:\leqslant\:\int_{{p}−\mathrm{1}} ^{{p}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\Rightarrow \\ $$$$\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\int_{{p}} ^{{p}+\mathrm{1}} \:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:{v}_{{p}} \:\:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \int_{{p}−\mathrm{1}} ^{{p}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]\:+\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:{v}_{{p}} \:\leqslant\:\:\int_{\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}}}\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{2}\sqrt{{x}}\right]_{\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]+\mathrm{1}} \:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} {v}_{{p}} \:\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{2}\sqrt{{x}}\right]_{\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\Rightarrow\:\sqrt{\mathrm{2}}\left\{\sqrt{\left[\frac{{n}}{\mathrm{2}}\right]+\mathrm{1}}−\mathrm{1}\right\}\leqslant\Sigma\:{v}_{{p}} \leqslant\sqrt{\mathrm{2}}\sqrt{\left[\frac{{n}}{\mathrm{2}}\right]} \\ $$$${also}\:\left({w}_{{p}} \right)\:{is}\:{decreasing}\:\Rightarrow\:\int_{{p}} ^{{p}+\mathrm{1}} \:\:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:\leqslant\:{w}_{{p}} \leqslant\:\int_{{p}−\mathrm{1}} ^{{p}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:\Rightarrow \\ $$$$\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\int_{{p}} ^{{p}+\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} {w}_{{p}} \:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\int_{{p}−\mathrm{1}} ^{{p}} \frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]\:+\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}+\mathrm{1}}}\:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:{w}_{{p}} \:\:\leqslant\:\int_{\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}\:+\mathrm{1}}}\:\Rightarrow \\ $$$$\left[\sqrt{\mathrm{2}{x}+\mathrm{1}}\right]_{\mathrm{1}} ^{\left.\frac{\left[{n}−\mathrm{1}\right.}{\mathrm{2}}\right]+\mathrm{1}} \:\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:{w}_{{p}} \:\leqslant\:\left[\sqrt{\mathrm{2}{x}+\mathrm{1}}\right]_{\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\Rightarrow \\ $$$$\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{2}}\:−\sqrt{\mathrm{3}}\leqslant\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:{w}_{{p}} \:\leqslant\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}}−\mathrm{1}\:\:\Rightarrow \\ $$$$\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{2}}+\mathrm{1}−\sqrt{\mathrm{3}}\leqslant\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:{w}_{{p}} \:\leqslant\:\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}}\:−\mathrm{2}\:\Rightarrow\: \\ $$$$\sqrt{\mathrm{2}}\left\{\sqrt{\left[\frac{{n}}{\mathrm{2}}\right]+\mathrm{1}}−\mathrm{1}\right\}\:+\mathrm{2}−\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}}\leqslant\:{u}_{{n}} \leqslant\:\sqrt{\mathrm{2}}\sqrt{\left[\frac{{n}}{\mathrm{2}}\right]}\:+\sqrt{\mathrm{3}}−\mathrm{1}−\sqrt{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \\ $$$$…{be}\:{continued}\:… \\ $$$$ \\ $$
