Question Number 42228 by rahul 19 last updated on 20/Aug/18
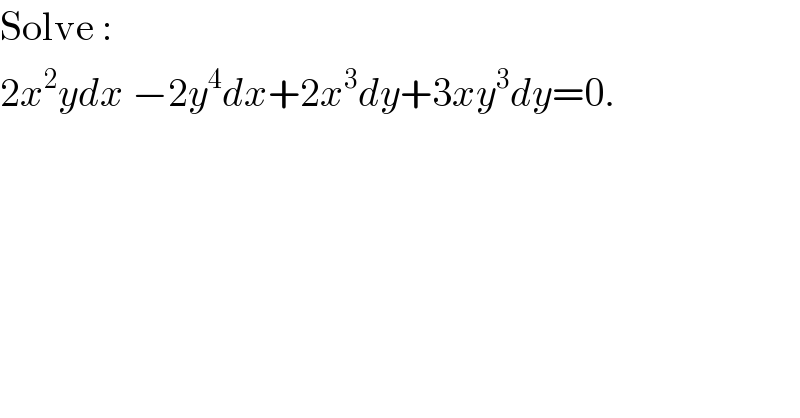
$$\mathrm{Solve}\:: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} {ydx}\:−\mathrm{2}{y}^{\mathrm{4}} {dx}+\mathrm{2}{x}^{\mathrm{3}} {dy}+\mathrm{3}{xy}^{\mathrm{3}} {dy}=\mathrm{0}. \\ $$
Answered by ajfour last updated on 20/Aug/18
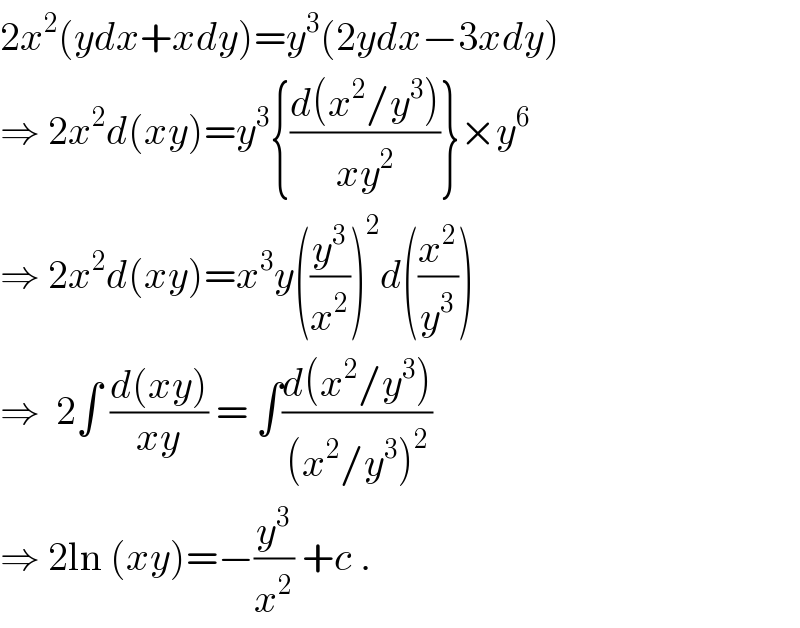
$$\mathrm{2}{x}^{\mathrm{2}} \left({ydx}+{xdy}\right)={y}^{\mathrm{3}} \left(\mathrm{2}{ydx}−\mathrm{3}{xdy}\right) \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} {d}\left({xy}\right)={y}^{\mathrm{3}} \left\{\frac{{d}\left({x}^{\mathrm{2}} /{y}^{\mathrm{3}} \right)}{{xy}^{\mathrm{2}} }\right\}×{y}^{\mathrm{6}} \\ $$$$\Rightarrow\:\mathrm{2}{x}^{\mathrm{2}} {d}\left({xy}\right)={x}^{\mathrm{3}} {y}\left(\frac{{y}^{\mathrm{3}} }{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} {d}\left(\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{3}} }\right) \\ $$$$\Rightarrow\:\:\mathrm{2}\int\:\frac{{d}\left({xy}\right)}{{xy}}\:=\:\int\frac{{d}\left({x}^{\mathrm{2}} /{y}^{\mathrm{3}} \right)}{\left({x}^{\mathrm{2}} /{y}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{2ln}\:\left({xy}\right)=−\frac{{y}^{\mathrm{3}} }{{x}^{\mathrm{2}} }\:+{c}\:. \\ $$
Commented by rahul 19 last updated on 20/Aug/18
Awesome ! ������
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Aug/18

$${excellent}… \\ $$
