Question Number 107790 by Ar Brandon last updated on 12/Aug/20
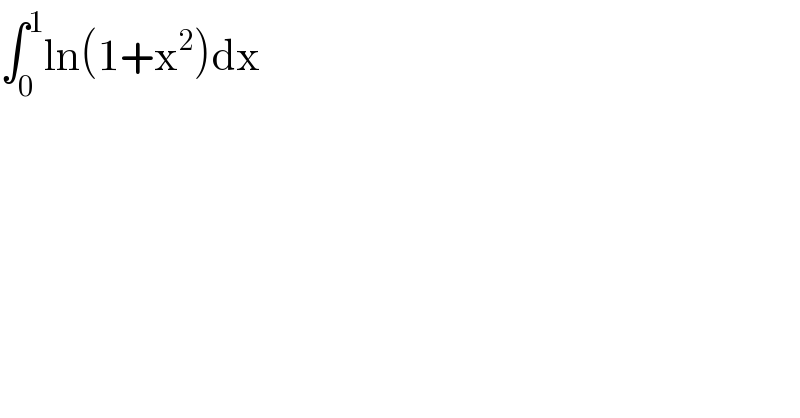
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$
Commented by prakash jain last updated on 12/Aug/20
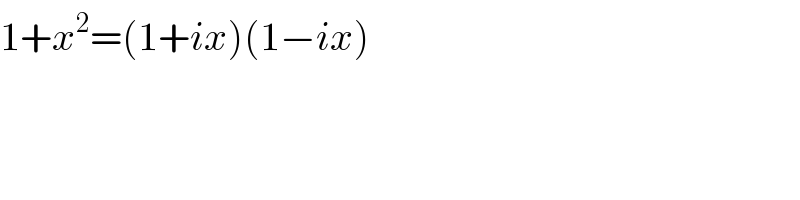
$$\mathrm{1}+{x}^{\mathrm{2}} =\left(\mathrm{1}+{ix}\right)\left(\mathrm{1}−{ix}\right) \\ $$
Commented by mohammad17 last updated on 12/Aug/20

$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right)=\left({i}+{x}\right)\left(−{i}+{x}\right) \\ $$
Commented by mohammad17 last updated on 12/Aug/20
![{ ((u=ln(1+x^2 )⇒u^′ =((2x)/(1+x^2 ))dx)),((v^′ =dx⇒v=x)) :} I=[xln(1+x^2 )]_0 ^1 −2∫_0 ^( 1) ((x^2 +1−1)/(1+x^2 ))dx I=[xln(1+x^2 )]_0 ^1 −[2x]_0 ^1 +[2tan^(−1) (x)]_0 ^1 I=ln(2)−2+(π/2) by: mss:Mohammad taha](https://www.tinkutara.com/question/Q107803.png)
$$\begin{cases}{{u}={ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\Rightarrow{u}^{'} =\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}}\\{{v}^{'} ={dx}\Rightarrow{v}={x}}\end{cases} \\ $$$$ \\ $$$${I}=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$${I}=\left[{xln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\left[\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\mathrm{2}{tan}^{−\mathrm{1}} \left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$ \\ $$$${I}={ln}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$$${by}:\:{mss}:{Mohammad}\:{taha} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
Thanks Sir
Commented by Ar Brandon last updated on 12/Aug/20
Thank you
Answered by mathmax by abdo last updated on 12/Aug/20
![I =∫_0 ^1 ln(1+x^2 )dx by parts I=[xln(1+x^2 )]_0 ^1 −∫_0 ^1 x.((2x)/(1+x^2 ))dx =ln(2)−2 ∫_0 ^1 ((1+x^2 −1)/(1+x^2 ))dx =ln(2)−2 +2 ∫_0 ^1 (dx/(1+x^2 )) =ln(2)−2 +2[arctanx]_0 ^1 =ln(2)−2+2((π/4)) ⇒ I =ln(2)−2 +(π/2)](https://www.tinkutara.com/question/Q107802.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{I}=\left[\mathrm{xln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}.\frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\mathrm{2}\left[\mathrm{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{2}\:+\frac{\pi}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
Merci monsieur��
Commented by mathmax by abdo last updated on 13/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by hgrocks last updated on 12/Aug/20
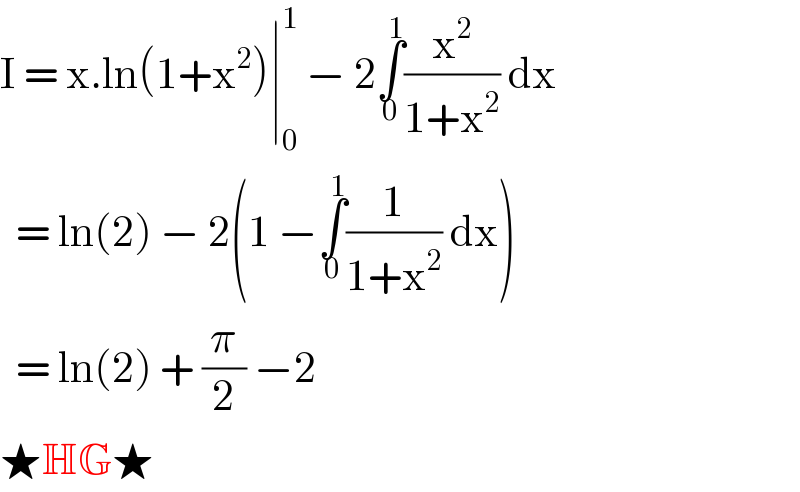
$$\mathrm{I}\:=\:\mathrm{x}.\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\:\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx} \\ $$$$\:\:=\:\mathrm{ln}\left(\mathrm{2}\right)\:−\:\mathrm{2}\left(\mathrm{1}\:−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\right) \\ $$$$\:\:=\:\mathrm{ln}\left(\mathrm{2}\right)\:+\:\frac{\pi}{\mathrm{2}}\:−\mathrm{2} \\ $$$$\bigstar\mathbb{HG}\bigstar \\ $$
Answered by Dwaipayan Shikari last updated on 12/Aug/20
![[xlog(1+x^2 )]_0 ^1 −2∫_0 ^1 (x^2 /(1+x^2 )) log(2)−2∫_0 ^1 1−(1/(1+x^2 )) log(2)−2+(π/2)](https://www.tinkutara.com/question/Q107808.png)
$$\left[{xlog}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${log}\left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${log}\left(\mathrm{2}\right)−\mathrm{2}+\frac{\pi}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
Hi ���� Thanks
Commented by Dwaipayan Shikari last updated on 12/Aug/20
����
Answered by hgrocks last updated on 12/Aug/20
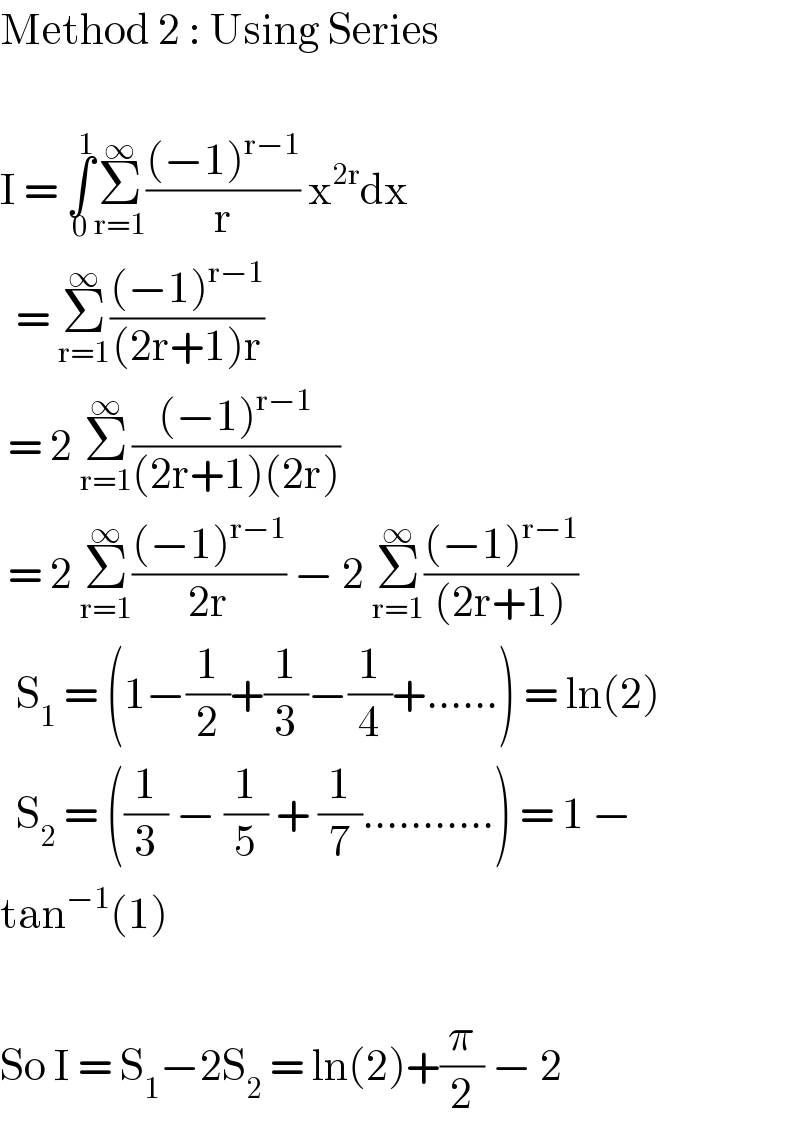
$$\mathrm{Method}\:\mathrm{2}\::\:\mathrm{Using}\:\mathrm{Series} \\ $$$$ \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} }{\mathrm{r}}\:\mathrm{x}^{\mathrm{2r}} \mathrm{dx} \\ $$$$\:\:=\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} }{\left(\mathrm{2r}+\mathrm{1}\right)\mathrm{r}} \\ $$$$\:=\:\mathrm{2}\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} }{\left(\mathrm{2r}+\mathrm{1}\right)\left(\mathrm{2r}\right)} \\ $$$$\:=\:\mathrm{2}\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} }{\mathrm{2r}}\:−\:\mathrm{2}\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{r}−\mathrm{1}} }{\left(\mathrm{2r}+\mathrm{1}\right)} \\ $$$$\:\:\mathrm{S}_{\mathrm{1}} \:=\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+……\right)\:=\:\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$\:\:\mathrm{S}_{\mathrm{2}} \:=\:\left(\frac{\mathrm{1}}{\mathrm{3}}\:−\:\frac{\mathrm{1}}{\mathrm{5}}\:+\:\frac{\mathrm{1}}{\mathrm{7}}………..\right)\:=\:\mathrm{1}\:− \\ $$$$\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{So}\:\mathrm{I}\:=\:\mathrm{S}_{\mathrm{1}} −\mathrm{2S}_{\mathrm{2}} \:=\:\mathrm{ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{2}}\:−\:\mathrm{2} \\ $$
Commented by Ar Brandon last updated on 12/Aug/20
Brilliant ! Redmiiuser��
