Question Number 107852 by mathdave last updated on 12/Aug/20
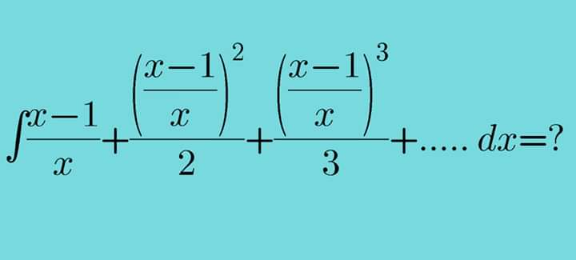
Answered by hgrocks last updated on 13/Aug/20
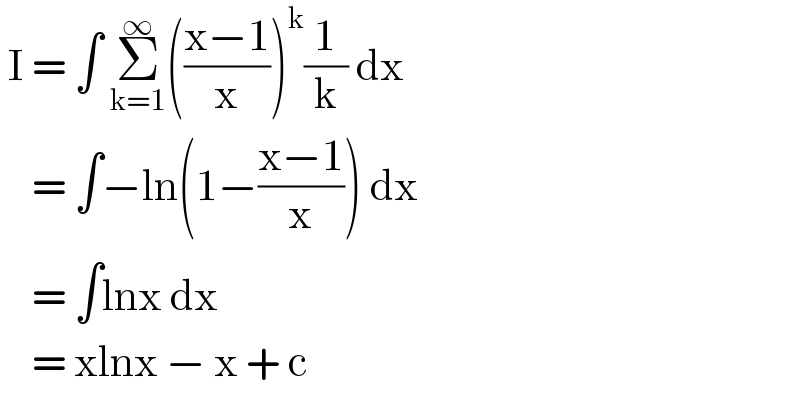
$$\:\mathrm{I}\:=\:\int\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{k}} \frac{\mathrm{1}}{\mathrm{k}}\:\mathrm{dx} \\ $$$$\:\:\:\:=\:\int−\mathrm{ln}\left(\mathrm{1}−\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}}\right)\:\mathrm{dx} \\ $$$$\:\:\:\:=\:\int\mathrm{lnx}\:\mathrm{dx} \\ $$$$\:\:\:\:=\:\mathrm{xlnx}\:−\:\mathrm{x}\:+\:\mathrm{c} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Aug/20
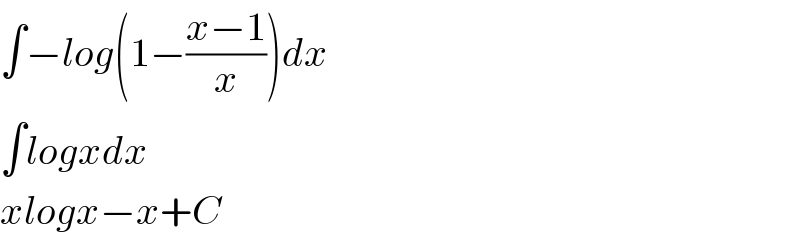
$$\int−{log}\left(\mathrm{1}−\frac{{x}−\mathrm{1}}{{x}}\right){dx} \\ $$$$\int{logxdx} \\ $$$${xlogx}−{x}+{C} \\ $$
