Menu Close

let-f-x-0-arctan-xt-2-cos-t-2-dt-1-find-a-explicite-form-of-f-x-2-find-a-explicite-form-of-f-x-3-find-the-value-of-0-cos-t-2-arctan-t-2-dt-and-0-cos-t-2-arc

Tinku Tara 0 Comments
Pin




Question Number 42374 by maxmathsup by imad last updated on 24/Aug/18
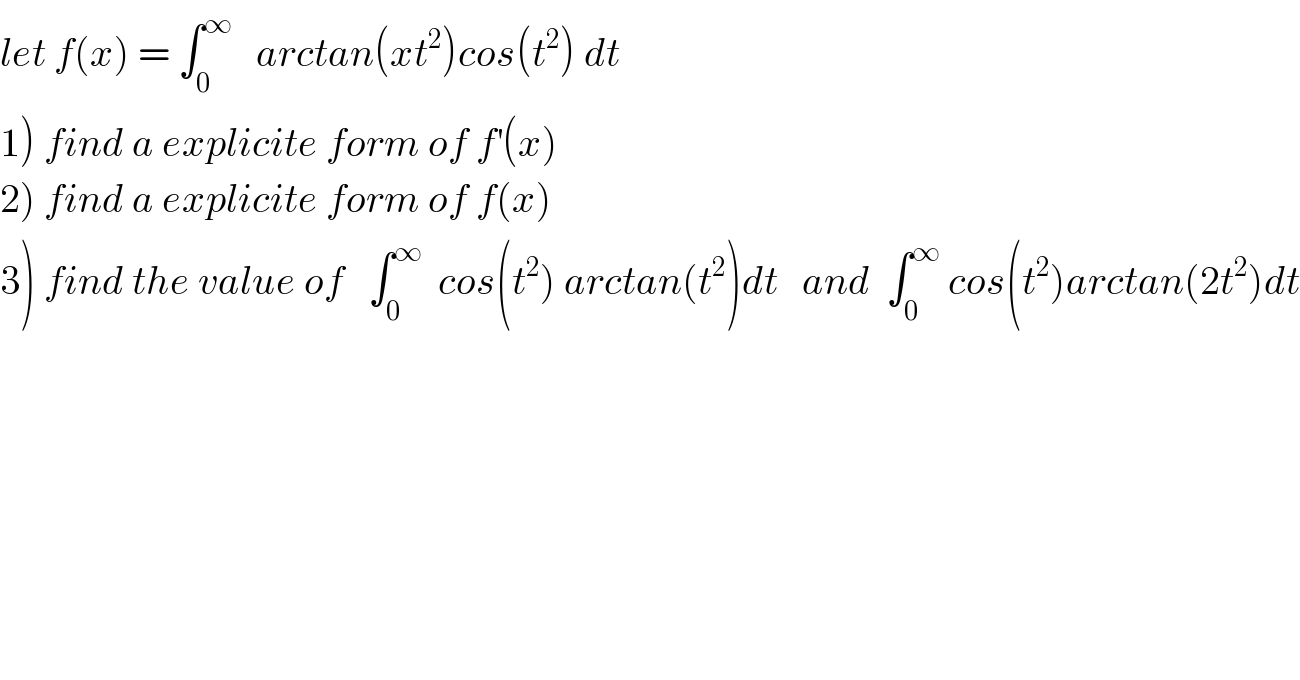
let f(x) = ∫_0 ^∞ arctan(xt^2 )cos(t^2 ) dt 1) find a explicite form of f^′ (x) 2) find a explicite form of f(x) 3) find the value of ∫_0 ^∞ cos(t^2 ) arctan(t^2 )dt and ∫_0 ^∞ cos(t^2 )arctan(2t^2 )dt
$${let}\:{f}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:{arctan}\left({xt}^{\mathrm{2}} \right){cos}\left({t}^{\mathrm{2}} \right)\:{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicite}\:{form}\:{of}\:{f}^{'} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{explicite}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{cos}\left({t}^{\mathrm{2}} \right)\:{arctan}\left({t}^{\mathrm{2}} \right){dt}\:\:\:{and}\:\:\int_{\mathrm{0}} ^{\infty} \:{cos}\left({t}^{\mathrm{2}} \right){arctan}\left(\mathrm{2}{t}^{\mathrm{2}} \right){dt} \\ $$
Commented by maxmathsup by imad last updated on 26/Aug/18
1) we have f(x)=∫_0 ^∞ arctan(xt^2 )cos(t^2 )dt ⇒ f^′ (x) =∫_0 ^∞ (t^2 /(1+x^2 t^4 )) cos(t^2 ) dt ⇒2f^′ (x) = ∫_(−∞) ^(+∞) ((t^2 cos(t^2 ))/(1+x^2 t^4 ))dt =Re( ∫_(−∞) ^(+∞) ((t^2 e^(it^2 ) )/(1+x^2 t^4 )))dt let consider the complex function ϕ(z) =((z^2 e^(iz^2 ) )/(x^2 z^4 +1)) we have ϕ(z) =((z^2 e^(iz^2 ) )/((xz^2 −i)(xz^2 +i))) =((z^2 e^(iz^2 ) )/(x^2 (z^2 −(i/x))(z^2 +(i/x)))) if x>0 we get ϕ(z) =((z^2 e^(iz^2 ) )/(x^2 (z−(1/( (√x)))e^((iπ)/4) )(z+(1/( (√x)))e^((iπ)/4) )(z −(1/( (√x))) e^(−((iπ)/4)) )(z + (1/( (√x))) e^(−((iπ)/4)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,(1/( (√x)))e^((iπ)/4) ) +Res(ϕ,−(1/( (√x))) e^(−((iπ)/4)) )} Res(ϕ, (1/( (√x))) e^((iπ)/4) ) =(((1/x)ie^(i(1/x)i) )/(x^2 ((2/( (√x)))e^((iπ)/4) )(2 (i/x)))) = (((√x)e^(−(1/x)) )/(4x^2 e^((iπ)/4) )) =((√x)/(4x^2 )) e^(−(1/x)−((iπ)/4)) =(1/4) (e^(−(1/x)) /(x(√x))) e^(−((iπ)/4)) Res(ϕ,−(1/( (√x))) e^(−((iπ)/4)) ) = (((((−i)/x))e^(i(−(i/x))) )/(x^2 (((−2i)/x))(((−2)/( (√x)))e^(−((iπ)/4)) ))) =−(1/4) (e^(1/x) /(x(√x))) e^((iπ)/4) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =((2iπ)/(4x(√x))){ e^(−(1/(x ))−((iπ)/4)) − e^((1/x) +((iπ)/4)) }=−((iπ)/(2x(√x))){ e^((1/x) +((iπ)/4)) −e^(−(1/x)−((iπ)/4)) } =−((iπ)/(2x(√x))){2i Im(e^((1/x)+((iπ)/4)) )} = (π/(x(√x))) (1/( (√2))) e^(1/x) ⇒2f^′ (x)= (π/(x(√(2x)))) e^(1/x) ⇒ f^′ (x) = (π/(2x(√(2x)))) e^(1/x) ⇒ f(x) = ∫^x (π/(2t(√(2t)))) e^(1/t) dt +c. ....be continued...
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:{arctan}\left({xt}^{\mathrm{2}} \right){cos}\left({t}^{\mathrm{2}} \right){dt}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} }\:{cos}\left({t}^{\mathrm{2}} \right)\:{dt}\:\Rightarrow\mathrm{2}{f}^{'} \left({x}\right)\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{t}^{\mathrm{2}} \:{cos}\left({t}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} }{dt} \\ $$$$={Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{t}^{\mathrm{2}} \:{e}^{{it}^{\mathrm{2}} } }{\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{4}} }\right){dt}\:\:{let}\:{consider}\:{the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:{e}^{{iz}^{\mathrm{2}} } }{{x}^{\mathrm{2}} {z}^{\mathrm{4}} \:+\mathrm{1}}\:\:{we}\:{have}\:\varphi\left({z}\right)\:\:=\frac{{z}^{\mathrm{2}} \:{e}^{{iz}^{\mathrm{2}} } }{\left({xz}^{\mathrm{2}} −{i}\right)\left({xz}^{\mathrm{2}} \:+{i}\right)} \\ $$$$=\frac{{z}^{\mathrm{2}} \:{e}^{{iz}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \left({z}^{\mathrm{2}} \:−\frac{{i}}{{x}}\right)\left({z}^{\mathrm{2}} \:+\frac{{i}}{{x}}\right)}\:\:\:{if}\:{x}>\mathrm{0}\:\:{we}\:{get}\: \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} \:{e}^{{iz}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \left({z}−\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}\:−\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}\:+\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,\frac{\mathrm{1}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{Res}\left(\varphi,−\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left(\varphi,\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{\frac{\mathrm{1}}{\boldsymbol{{x}}}{ie}^{{i}\frac{\mathrm{1}}{{x}}{i}} }{\boldsymbol{{x}}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\:\sqrt{{x}}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left(\mathrm{2}\:\frac{{i}}{{x}}\right)}\:=\:\frac{\sqrt{{x}}{e}^{−\frac{\mathrm{1}}{{x}}} }{\mathrm{4}{x}^{\mathrm{2}} {e}^{\frac{{i}\pi}{\mathrm{4}}} }\:=\frac{\sqrt{{x}}}{\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }\:{e}^{−\frac{\mathrm{1}}{{x}}−\frac{{i}\pi}{\mathrm{4}}} \:\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{e}^{−\frac{\mathrm{1}}{{x}}} }{{x}\sqrt{{x}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${Res}\left(\varphi,−\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:\:=\:\frac{\left(\frac{−{i}}{{x}}\right){e}^{{i}\left(−\frac{{i}}{{x}}\right)} }{{x}^{\mathrm{2}} \left(\frac{−\mathrm{2}{i}}{{x}}\right)\left(\frac{−\mathrm{2}}{\:\sqrt{{x}}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{e}^{\frac{\mathrm{1}}{{x}}} }{{x}\sqrt{{x}}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\mathrm{2}{i}\pi}{\mathrm{4}{x}\sqrt{{x}}}\left\{\:{e}^{−\frac{\mathrm{1}}{{x}\:}−\frac{{i}\pi}{\mathrm{4}}} \:\:−\:{e}^{\frac{\mathrm{1}}{{x}}\:+\frac{{i}\pi}{\mathrm{4}}} \right\}=−\frac{{i}\pi}{\mathrm{2}{x}\sqrt{{x}}}\left\{\:{e}^{\frac{\mathrm{1}}{{x}}\:+\frac{{i}\pi}{\mathrm{4}}} \:−{e}^{−\frac{\mathrm{1}}{{x}}−\frac{{i}\pi}{\mathrm{4}}} \right\} \\ $$$$=−\frac{{i}\pi}{\mathrm{2}{x}\sqrt{{x}}}\left\{\mathrm{2}{i}\:{Im}\left({e}^{\frac{\mathrm{1}}{{x}}+\frac{{i}\pi}{\mathrm{4}}} \right)\right\}\:=\:\frac{\pi}{{x}\sqrt{{x}}}\:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:{e}^{\frac{\mathrm{1}}{{x}}} \:\Rightarrow\mathrm{2}{f}^{'} \left({x}\right)=\:\frac{\pi}{{x}\sqrt{\mathrm{2}{x}}}\:{e}^{\frac{\mathrm{1}}{{x}}} \:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\pi}{\mathrm{2}{x}\sqrt{\mathrm{2}{x}}}\:{e}^{\frac{\mathrm{1}}{{x}}} \:\Rightarrow\:{f}\left({x}\right)\:=\:\int^{{x}} \:\:\:\frac{\pi}{\mathrm{2}{t}\sqrt{\mathrm{2}{t}}}\:{e}^{\frac{\mathrm{1}}{{t}}} \:{dt}\:+{c}.\:\:….{be}\:{continued}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *