Question Number 42492 by maxmathsup by imad last updated on 26/Aug/18
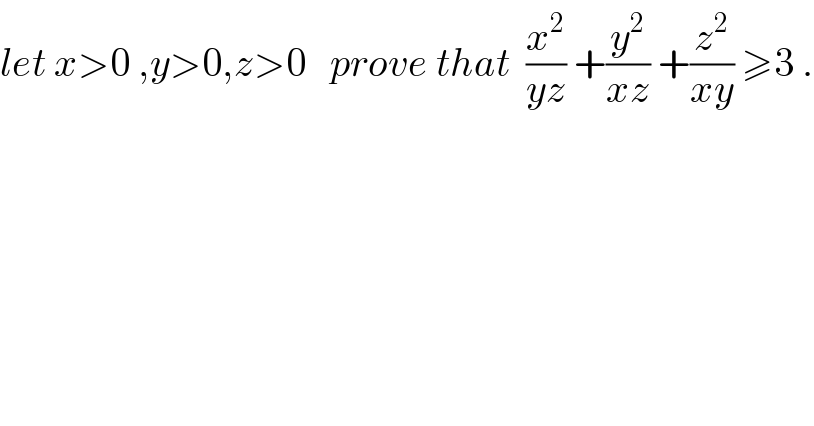
$${let}\:{x}>\mathrm{0}\:,{y}>\mathrm{0},{z}>\mathrm{0}\:\:\:{prove}\:{that}\:\:\frac{{x}^{\mathrm{2}} }{{yz}}\:+\frac{{y}^{\mathrm{2}} }{{xz}}\:+\frac{{z}^{\mathrm{2}} }{{xy}}\:\geqslant\mathrm{3}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Aug/18
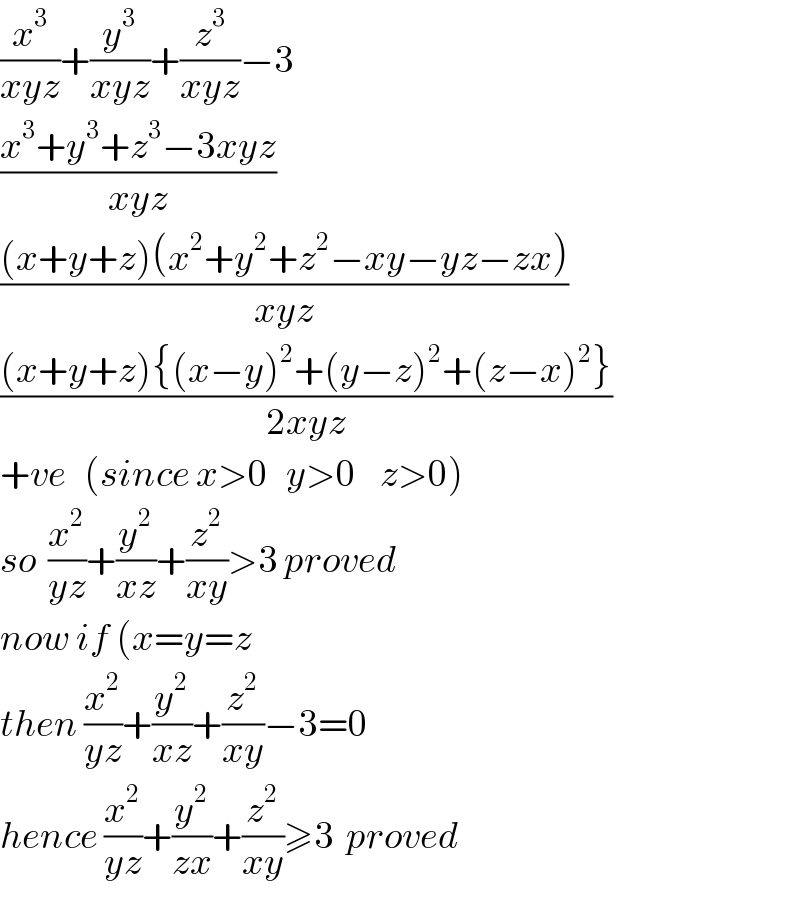
$$\frac{{x}^{\mathrm{3}} }{{xyz}}+\frac{{y}^{\mathrm{3}} }{{xyz}}+\frac{{z}^{\mathrm{3}} }{{xyz}}−\mathrm{3} \\ $$$$\frac{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} +{z}^{\mathrm{3}} −\mathrm{3}{xyz}}{{xyz}} \\ $$$$\frac{\left({x}+{y}+{z}\right)\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{xy}−{yz}−{zx}\right)}{{xyz}} \\ $$$$\frac{\left({x}+{y}+{z}\right)\left\{\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} \right\}}{\mathrm{2}{xyz}} \\ $$$$+{ve}\:\:\:\left({since}\:{x}>\mathrm{0}\:\:\:{y}>\mathrm{0}\:\:\:\:{z}>\mathrm{0}\right) \\ $$$${so}\:\:\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{xz}}+\frac{{z}^{\mathrm{2}} }{{xy}}>\mathrm{3}\:{proved} \\ $$$${now}\:{if}\:\left({x}={y}={z}\right. \\ $$$${then}\:\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{xz}}+\frac{{z}^{\mathrm{2}} }{{xy}}−\mathrm{3}=\mathrm{0} \\ $$$${hence}\:\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{zx}}+\frac{{z}^{\mathrm{2}} }{{xy}}\geqslant\mathrm{3}\:\:{proved} \\ $$
Commented by math khazana by abdo last updated on 27/Aug/18
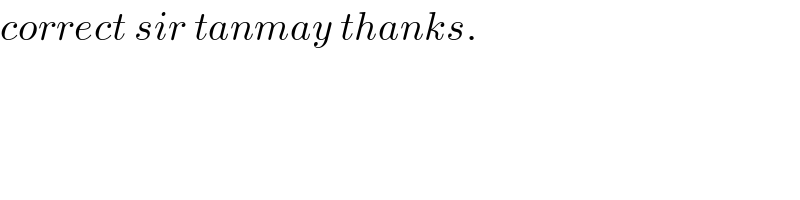
$${correct}\:{sir}\:{tanmay}\:{thanks}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Aug/18

$${its}\:{ok}\:{sir} \\ $$
Answered by behi83417@gmail.com last updated on 26/Aug/18
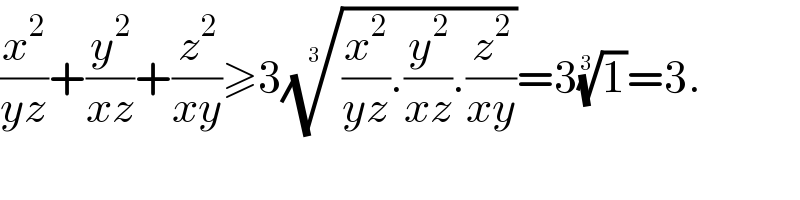
$$\frac{{x}^{\mathrm{2}} }{{yz}}+\frac{{y}^{\mathrm{2}} }{{xz}}+\frac{{z}^{\mathrm{2}} }{{xy}}\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\frac{{x}^{\mathrm{2}} }{{yz}}.\frac{{y}^{\mathrm{2}} }{{xz}}.\frac{{z}^{\mathrm{2}} }{{xy}}}=\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{1}}=\mathrm{3}. \\ $$
