Question Number 42501 by maxmathsup by imad last updated on 26/Aug/18
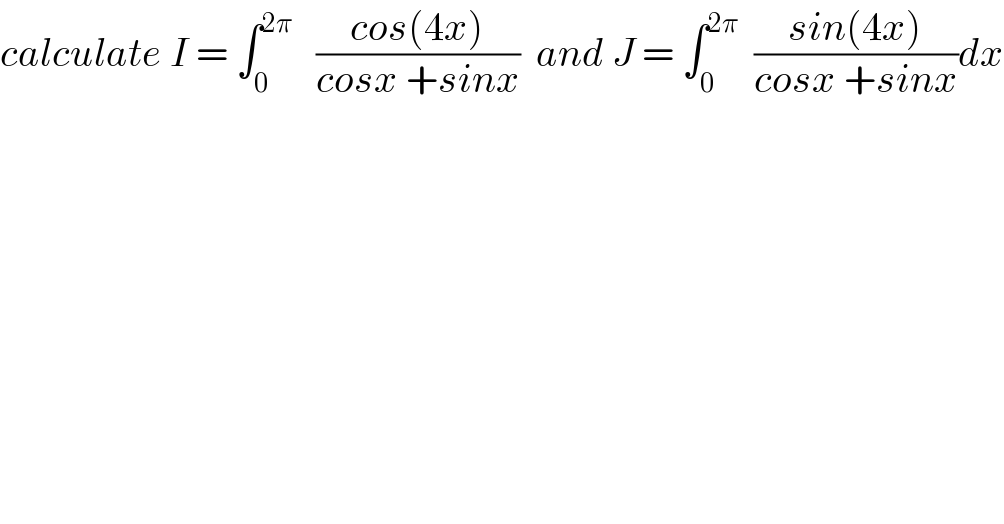
$${calculate}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{cosx}\:+{sinx}}\:\:{and}\:{J}\:=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{sin}\left(\mathrm{4}{x}\right)}{{cosx}\:+{sinx}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 27/Aug/18
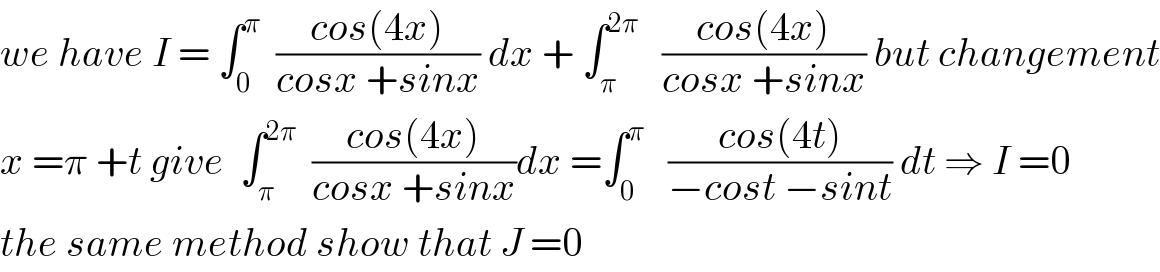
$${we}\:{have}\:{I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{cosx}\:+{sinx}}\:{dx}\:+\:\int_{\pi} ^{\mathrm{2}\pi} \:\:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{cosx}\:+{sinx}}\:{but}\:{changement} \\ $$$${x}\:=\pi\:+{t}\:{give}\:\:\int_{\pi} ^{\mathrm{2}\pi} \:\:\frac{{cos}\left(\mathrm{4}{x}\right)}{{cosx}\:+{sinx}}{dx}\:=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{cos}\left(\mathrm{4}{t}\right)}{−{cost}\:−{sint}}\:{dt}\:\Rightarrow\:{I}\:=\mathrm{0} \\ $$$${the}\:{same}\:{method}\:{show}\:{that}\:{J}\:=\mathrm{0} \\ $$
