Question Number 108043 by ZiYangLee last updated on 14/Aug/20
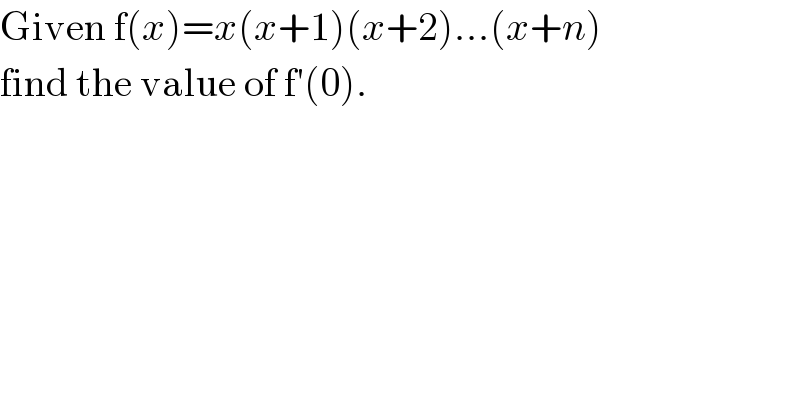
$$\mathrm{Given}\:\mathrm{f}\left({x}\right)={x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)…\left({x}+{n}\right) \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{f}'\left(\mathrm{0}\right). \\ $$
Answered by hgrocks last updated on 14/Aug/20
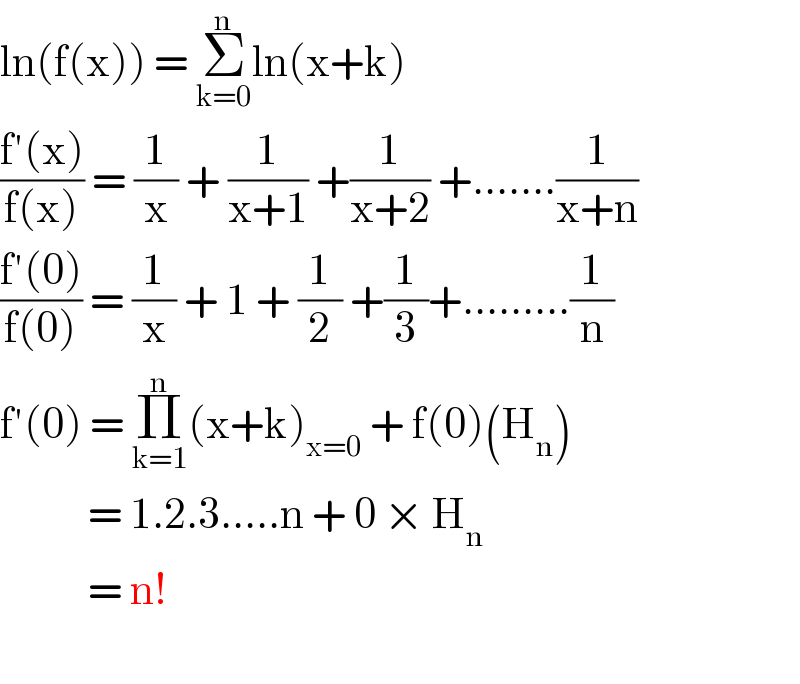
$$\mathrm{ln}\left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{x}+\mathrm{k}\right) \\ $$$$\frac{\mathrm{f}'\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{x}+\mathrm{2}}\:+…….\frac{\mathrm{1}}{\mathrm{x}+\mathrm{n}} \\ $$$$\frac{\mathrm{f}'\left(\mathrm{0}\right)}{\mathrm{f}\left(\mathrm{0}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{x}}\:+\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}+………\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\mathrm{f}'\left(\mathrm{0}\right)\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{x}+\mathrm{k}\right)_{\mathrm{x}=\mathrm{0}} \:+\:\mathrm{f}\left(\mathrm{0}\right)\left(\mathrm{H}_{\mathrm{n}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}.\mathrm{2}.\mathrm{3}…..\mathrm{n}\:+\:\mathrm{0}\:×\:\mathrm{H}_{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{n}! \\ $$$$ \\ $$
Commented by ZiYangLee last updated on 14/Aug/20

$$\mathrm{wow}… \\ $$
Answered by Her_Majesty last updated on 14/Aug/20
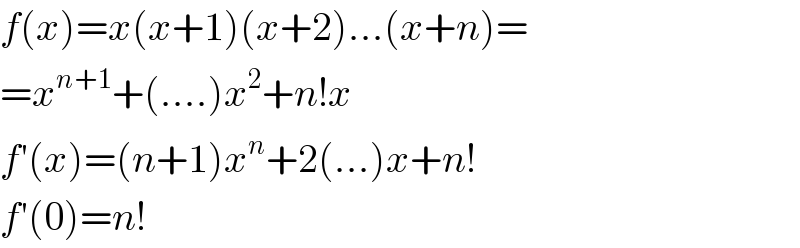
$${f}\left({x}\right)={x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)…\left({x}+{n}\right)= \\ $$$$={x}^{{n}+\mathrm{1}} +\left(….\right){x}^{\mathrm{2}} +{n}!{x} \\ $$$${f}'\left({x}\right)=\left({n}+\mathrm{1}\right){x}^{{n}} +\mathrm{2}\left(…\right){x}+{n}! \\ $$$${f}'\left(\mathrm{0}\right)={n}! \\ $$
