Question Number 42507 by maxmathsup by imad last updated on 26/Aug/18
![let j =e^((i2π)/3) and p(x) =(1+xj)^n −(1−xj)^n 1) find the roots of p(x) and factorize inside C[x] p(x) 2) decompose inside C(x) the fration F(x) =(1/(p(x))) .](https://www.tinkutara.com/question/Q42507.png)
$${let}\:{j}\:={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\:\:{and}\:\:\:{p}\left({x}\right)\:=\left(\mathrm{1}+{xj}\right)^{{n}} \:−\left(\mathrm{1}−{xj}\right)^{{n}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{the}\:{roots}\:{of}\:{p}\left({x}\right)\:{and}\:{factorize}\:{inside}\:{C}\left[{x}\right]\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{decompose}\:{inside}\:{C}\left({x}\right)\:{the}\:{fration}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{{p}\left({x}\right)}\:. \\ $$
Commented by maxmathsup by imad last updated on 28/Aug/18
![1) p(x)=0 ⇔ (((1+xj)/(1−xj)))^n =1 ⇒ ((1+xj)/(1−xj)) =e^((i2kπ)/n) k∈[[0,n−1]] let z_k =e^((i2kπ)/n) ⇒ ((1+xj)/(1−xj)) =z_k ⇒1+jx = z_k −jz_k x ⇒j(1+z_k )x = z_k −1 ⇒x =((z_k −1)/(j(1+z_k ))) =−(1/j) ((1−z_k )/(1+z_k )) ⇒ the roots are x_k =−(1/j) ((1−cos(((2kπ)/n))−isin(((2kπ)/n)))/(1+cos(((2kπ)/n))+isin(((2kπ)/n)))) =−(1/j) ((2sin^2 (((kπ)/n))−2isin(((kπ)/n))cos(((kπ)/n)))/(2cos^2 (((kπ)/n))+2i sin(((kπ)/n))cos(((kπ)/n)))) =(i/j) ((sin(((kπ)/n))(cos(((kπ)/n)) +isin(((kπ)/n))))/(cos(((kπ)/n))(cos(((kπ)/n))+isin(((kπ)/n))))) =(i/j)tan(((kπ)/n)) ⇒ x_k =(i/j) tan(((kπ)/n)) and 0≤k≤n−1 p(x) =λ Π_(k=0) ^(n−1) (x−x_k ) =λ Π_(k=0) ^(n−1) (x−(i/j)tan(((kπ)/n))) let findλ we have p(x) =Σ_(k=0) ^n C_n ^k j^k x^k −Σ_(k=0) ^(n−1) C_n ^k (−1)^k j^k x^k =Σ_(k=0) ^n C_n ^k {1−(−1)^k }j^k x^k ⇒λ = (1−(−1)^n )j^n ⇒ p(x) =(1−(−1)^n )j^n Π_(k=0) ^(n−1) (x−(i/j)tan(((kπ)/n))) .](https://www.tinkutara.com/question/Q42590.png)
$$\left.\mathrm{1}\right)\:{p}\left({x}\right)=\mathrm{0}\:\Leftrightarrow\:\left(\frac{\mathrm{1}+{xj}}{\mathrm{1}−{xj}}\right)^{{n}} \:=\mathrm{1}\:\:\:\Rightarrow\:\frac{\mathrm{1}+{xj}}{\mathrm{1}−{xj}}\:={e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\:\:\:\:\:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\:{let}\:{z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}+{xj}}{\mathrm{1}−{xj}}\:={z}_{{k}} \Rightarrow\mathrm{1}+{jx}\:=\:{z}_{{k}} \:−{jz}_{{k}} {x}\:\Rightarrow{j}\left(\mathrm{1}+{z}_{{k}} \right){x}\:=\:{z}_{{k}} −\mathrm{1}\:\Rightarrow{x}\:=\frac{{z}_{{k}} −\mathrm{1}}{{j}\left(\mathrm{1}+{z}_{{k}} \right)} \\ $$$$=−\frac{\mathrm{1}}{{j}}\:\frac{\mathrm{1}−{z}_{{k}} }{\mathrm{1}+{z}_{{k}} }\:\Rightarrow\:{the}\:{roots}\:{are}\:{x}_{{k}} =−\frac{\mathrm{1}}{{j}}\:\frac{\mathrm{1}−{cos}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)−{isin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)}{\mathrm{1}+{cos}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)+{isin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)} \\ $$$$=−\frac{\mathrm{1}}{{j}}\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{{n}}\right)−\mathrm{2}{isin}\left(\frac{{k}\pi}{{n}}\right){cos}\left(\frac{{k}\pi}{{n}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{k}\pi}{{n}}\right)+\mathrm{2}{i}\:{sin}\left(\frac{{k}\pi}{{n}}\right){cos}\left(\frac{{k}\pi}{{n}}\right)}\:=\frac{{i}}{{j}}\:\frac{{sin}\left(\frac{{k}\pi}{{n}}\right)\left({cos}\left(\frac{{k}\pi}{{n}}\right)\:+{isin}\left(\frac{{k}\pi}{{n}}\right)\right)}{{cos}\left(\frac{{k}\pi}{{n}}\right)\left({cos}\left(\frac{{k}\pi}{{n}}\right)+{isin}\left(\frac{{k}\pi}{{n}}\right)\right)} \\ $$$$=\frac{{i}}{{j}}{tan}\left(\frac{{k}\pi}{{n}}\right)\:\Rightarrow\:{x}_{{k}} \:=\frac{{i}}{{j}}\:{tan}\left(\frac{{k}\pi}{{n}}\right)\:{and}\:\:\mathrm{0}\leqslant{k}\leqslant{n}−\mathrm{1} \\ $$$${p}\left({x}\right)\:=\lambda\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)\:=\lambda\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−\frac{{i}}{{j}}{tan}\left(\frac{{k}\pi}{{n}}\right)\right)\:\:{let}\:{find}\lambda \\ $$$${we}\:{have}\:\:{p}\left({x}\right)\:=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} {j}^{{k}} \:{x}^{{k}} \:−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {j}^{{k}} {x}^{{k}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \left\{\mathrm{1}−\left(−\mathrm{1}\right)^{{k}} \right\}{j}^{{k}} \:{x}^{{k}} \:\Rightarrow\lambda\:\:=\:\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right){j}^{{n}} \:\Rightarrow \\ $$$${p}\left({x}\right)\:=\left(\mathrm{1}−\left(−\mathrm{1}\right)^{{n}} \right){j}^{{n}} \:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−\frac{{i}}{{j}}{tan}\left(\frac{{k}\pi}{{n}}\right)\right)\:. \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 28/Aug/18
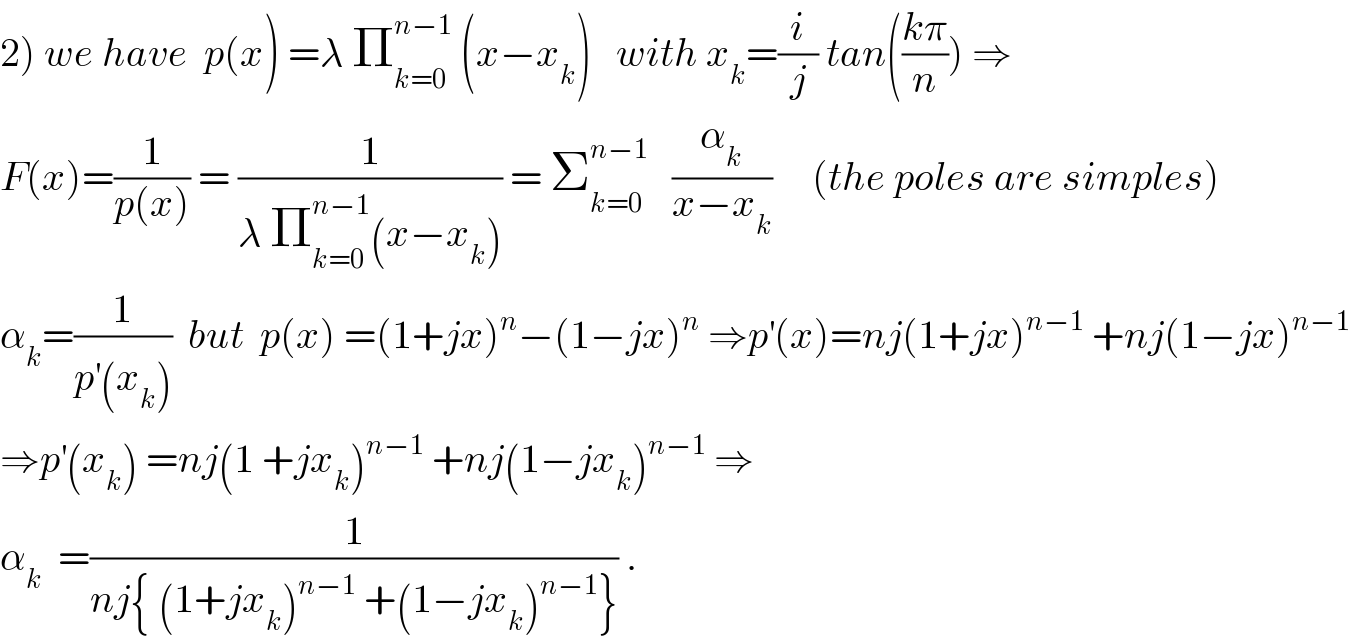
$$\left.\mathrm{2}\right)\:{we}\:{have}\:\:{p}\left({x}\right)\:=\lambda\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left({x}−{x}_{{k}} \right)\:\:\:{with}\:{x}_{{k}} =\frac{{i}}{{j}}\:{tan}\left(\frac{{k}\pi}{{n}}\right)\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{{p}\left({x}\right)}\:=\:\frac{\mathrm{1}}{\lambda\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)}\:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\alpha_{{k}} }{{x}−{x}_{{k}} }\:\:\:\:\:\left({the}\:{poles}\:{are}\:{simples}\right) \\ $$$$\alpha_{{k}} =\frac{\mathrm{1}}{{p}^{'} \left({x}_{{k}} \right)}\:\:{but}\:\:{p}\left({x}\right)\:=\left(\mathrm{1}+{jx}\right)^{{n}} −\left(\mathrm{1}−{jx}\right)^{{n}} \:\Rightarrow{p}^{'} \left({x}\right)={nj}\left(\mathrm{1}+{jx}\right)^{{n}−\mathrm{1}} \:+{nj}\left(\mathrm{1}−{jx}\right)^{{n}−\mathrm{1}} \\ $$$$\Rightarrow{p}^{'} \left({x}_{{k}} \right)\:={nj}\left(\mathrm{1}\:+{jx}_{{k}} \right)^{{n}−\mathrm{1}} \:+{nj}\left(\mathrm{1}−{jx}_{{k}} \right)^{{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\alpha_{{k}} \:\:=\frac{\mathrm{1}}{{nj}\left\{\:\left(\mathrm{1}+{jx}_{{k}} \right)^{{n}−\mathrm{1}} \:+\left(\mathrm{1}−{jx}_{{k}} \right)^{{n}−\mathrm{1}} \right\}}\:. \\ $$
