Question Number 4242 by prakash jain last updated on 05/Jan/16

$$\mathrm{Find}\:\mathrm{that}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{2}^{\mathrm{2}^{\mathrm{2}\centerdot\centerdot\centerdot} } \:\:\left(\mathrm{continued}\:\mathrm{power}\:\mathrm{of}\:\mathrm{2}\right) \\ $$$$\mathrm{using}\:\mathrm{analytical}\:\mathrm{continuation}. \\ $$
Commented by RasheedSindhi last updated on 06/Jan/16
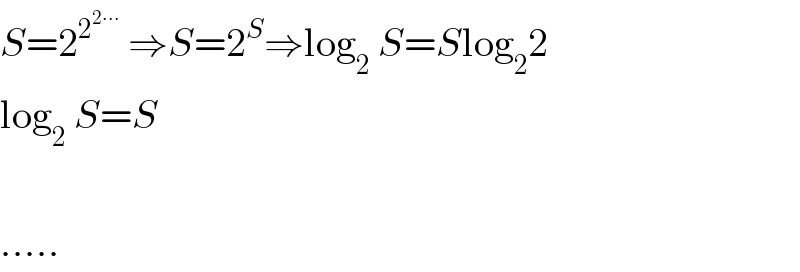
$${S}=\mathrm{2}^{\mathrm{2}^{\mathrm{2}\centerdot\centerdot\centerdot} } \:\Rightarrow{S}=\mathrm{2}^{{S}} \Rightarrow\mathrm{log}_{\mathrm{2}} \:{S}={S}\mathrm{log}_{\mathrm{2}} \mathrm{2}\: \\ $$$$\mathrm{log}_{\mathrm{2}} \:{S}={S} \\ $$$$ \\ $$$$….. \\ $$
Commented by Rasheed Soomro last updated on 06/Jan/16
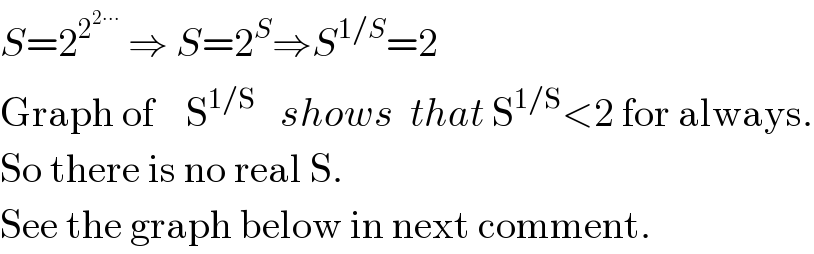
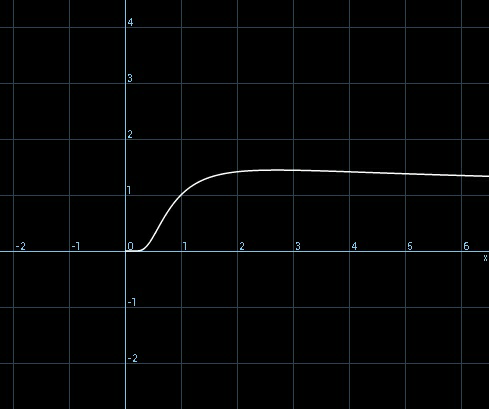
$${S}=\mathrm{2}^{\mathrm{2}^{\mathrm{2}\centerdot\centerdot\centerdot} } \:\Rightarrow\:{S}=\mathrm{2}^{{S}} \Rightarrow{S}^{\mathrm{1}/{S}} =\mathrm{2} \\ $$$$\mathrm{Graph}\:\mathrm{of}\:\:\:\:\mathrm{S}^{\mathrm{1}/\mathrm{S}} \:\:\:{shows}\:\:{that}\:\mathrm{S}^{\mathrm{1}/\mathrm{S}} <\mathrm{2}\:\mathrm{for}\:\mathrm{always}. \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{real}\:\mathrm{S}. \\ $$$$\mathrm{See}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{below}\:\mathrm{in}\:\mathrm{next}\:\mathrm{comment}. \\ $$
Commented by Filup last updated on 07/Jan/16
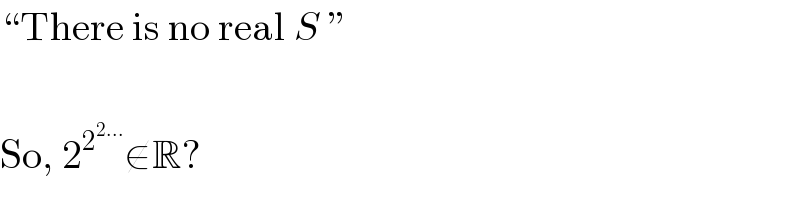
$$“\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{real}\:{S}\:'' \\ $$$$ \\ $$$$\mathrm{So},\:\mathrm{2}^{\mathrm{2}^{\mathrm{2}…} } \notin\mathbb{R}? \\ $$
Commented by Rasheed Soomro last updated on 06/Jan/16
Commented by Yozzii last updated on 07/Jan/16
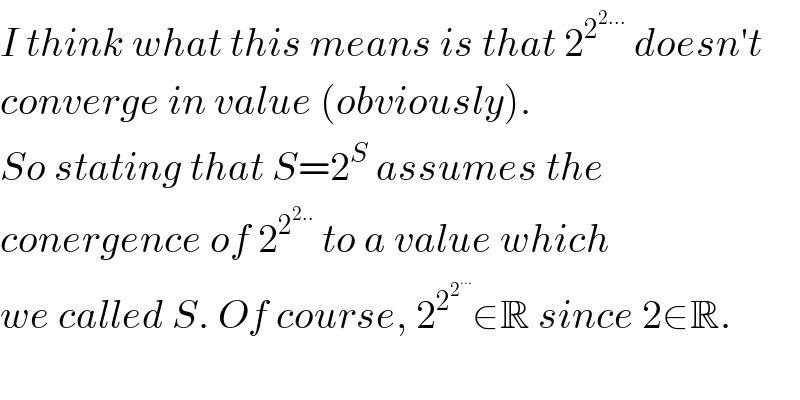
$${I}\:{think}\:{what}\:{this}\:{means}\:{is}\:{that}\:\mathrm{2}^{\mathrm{2}^{\mathrm{2}…} } \:{doesn}'{t} \\ $$$${converge}\:{in}\:{value}\:\left({obviously}\right). \\ $$$${So}\:{stating}\:{that}\:{S}=\mathrm{2}^{{S}} \:{assumes}\:{the} \\ $$$${conergence}\:{of}\:\mathrm{2}^{\mathrm{2}^{\mathrm{2}..} } \:{to}\:{a}\:{value}\:{which} \\ $$$${we}\:{called}\:{S}.\:{Of}\:{course},\:\mathrm{2}^{\mathrm{2}^{\mathrm{2}^{…} } } \in\mathbb{R}\:{since}\:\mathrm{2}\in\mathbb{R}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 07/Jan/16
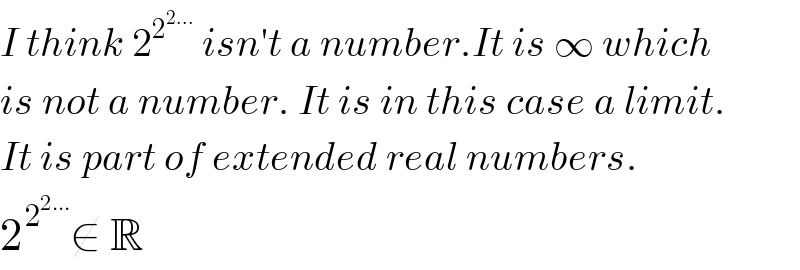
$${I}\:{think}\:\mathrm{2}^{\mathrm{2}^{\mathrm{2}…} } \:{isn}'{t}\:{a}\:{number}.{It}\:{is}\:\infty\:{which} \\ $$$${is}\:{not}\:{a}\:{number}.\:{It}\:{is}\:{in}\:{this}\:{case}\:{a}\:{limit}. \\ $$$${It}\:{is}\:{part}\:{of}\:{extended}\:{real}\:{numbers}. \\ $$$$\mathrm{2}^{\mathrm{2}^{\mathrm{2}…} } \notin\:\mathbb{R} \\ $$
Commented by Yozzii last updated on 07/Jan/16
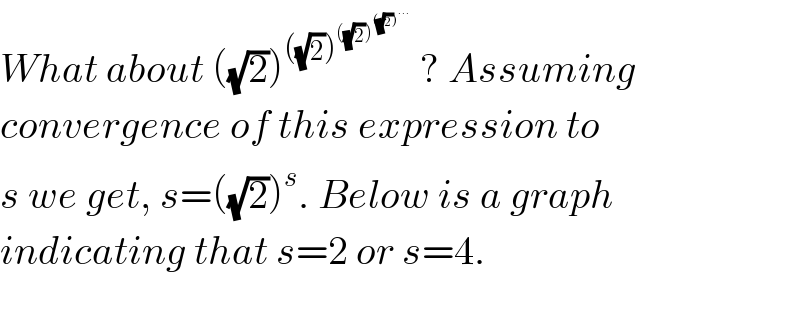
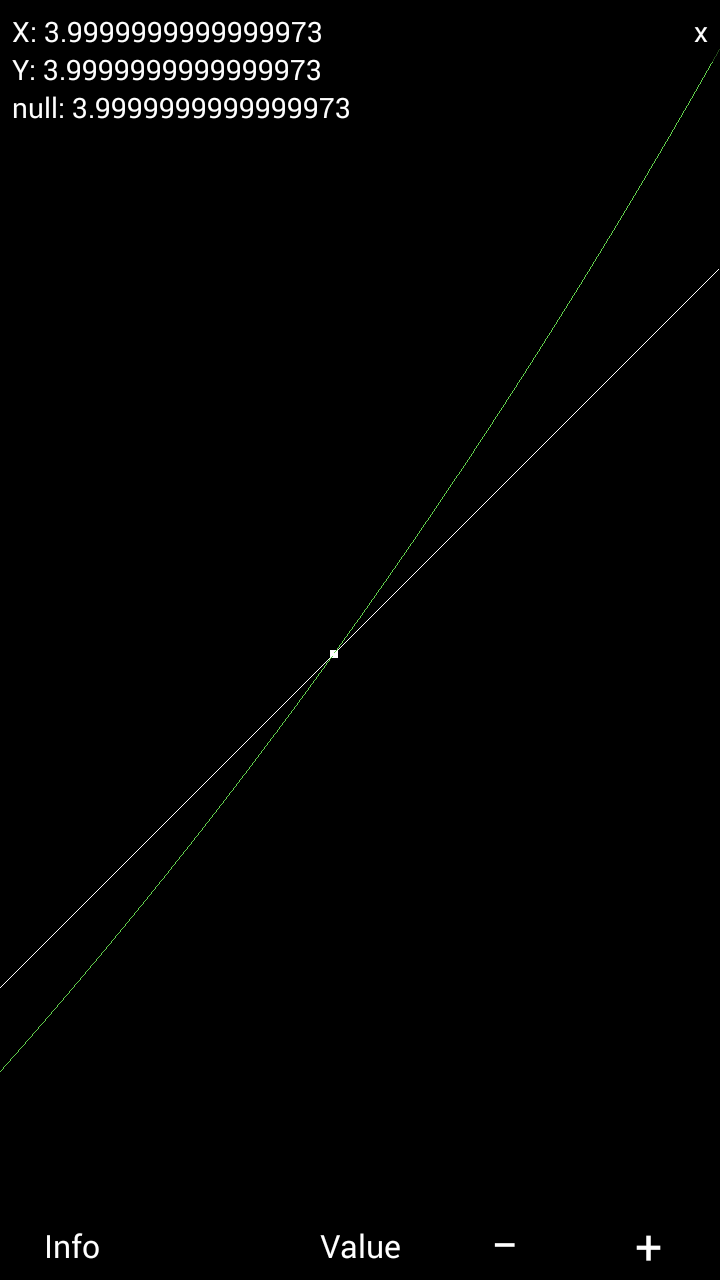
$${What}\:{about}\:\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{\left(\sqrt{\mathrm{2}}\right)^{…} } } } \:?\:{Assuming} \\ $$$${convergence}\:{of}\:{this}\:{expression}\:{to}\: \\ $$$${s}\:{we}\:{get},\:{s}=\left(\sqrt{\mathrm{2}}\right)^{{s}} .\:{Below}\:{is}\:{a}\:{graph} \\ $$$${indicating}\:{that}\:{s}=\mathrm{2}\:{or}\:{s}=\mathrm{4}. \\ $$$$ \\ $$
Commented by Yozzii last updated on 07/Jan/16

Commented by Yozzii last updated on 07/Jan/16
Commented by prakash jain last updated on 07/Jan/16
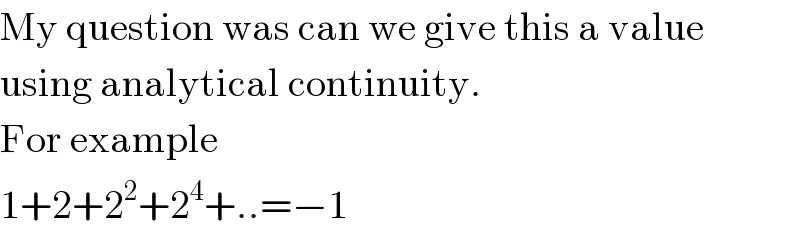
$$\mathrm{My}\:\mathrm{question}\:\mathrm{was}\:\mathrm{can}\:\mathrm{we}\:\mathrm{give}\:\mathrm{this}\:\mathrm{a}\:\mathrm{value} \\ $$$$\mathrm{using}\:\mathrm{analytical}\:\mathrm{continuity}. \\ $$$$\mathrm{For}\:\mathrm{example} \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{4}} +..=−\mathrm{1} \\ $$
Commented by 123456 last updated on 08/Jan/16
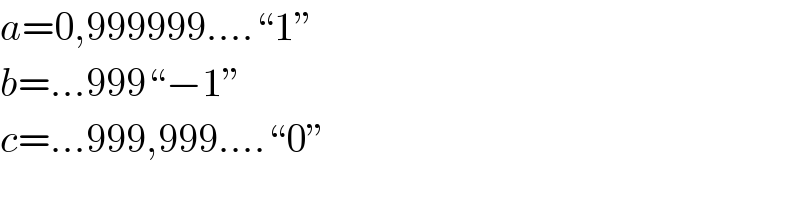
$${a}=\mathrm{0},\mathrm{999999}….“\mathrm{1}'' \\ $$$${b}=…\mathrm{999}“−\mathrm{1}'' \\ $$$${c}=…\mathrm{999},\mathrm{999}….“\mathrm{0}'' \\ $$
