Question Number 108082 by ismoilov last updated on 14/Aug/20
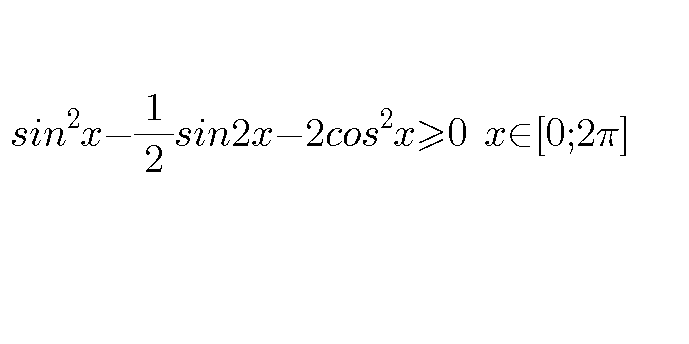
Answered by Her_Majesty last updated on 14/Aug/20
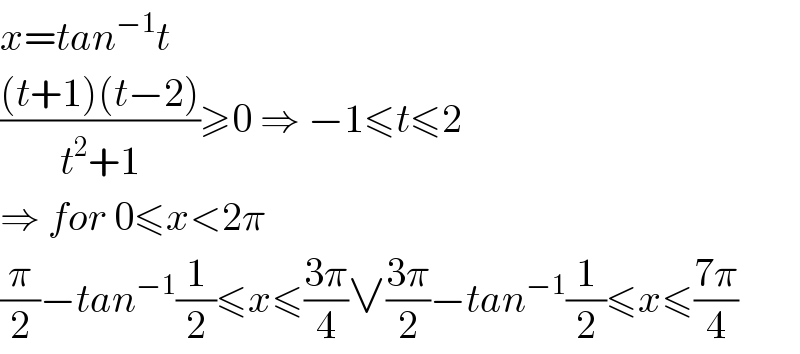
$${x}={tan}^{−\mathrm{1}} {t} \\ $$$$\frac{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{2}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}\geqslant\mathrm{0}\:\Rightarrow\:−\mathrm{1}\leqslant{t}\leqslant\mathrm{2} \\ $$$$\Rightarrow\:{for}\:\mathrm{0}\leqslant{x}<\mathrm{2}\pi \\ $$$$\frac{\pi}{\mathrm{2}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\frac{\mathrm{3}\pi}{\mathrm{4}}\vee\frac{\mathrm{3}\pi}{\mathrm{2}}−{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\frac{\mathrm{7}\pi}{\mathrm{4}} \\ $$
Commented by Jamshidbek2311 last updated on 14/Aug/20

$${thank}\:{you} \\ $$
