Question Number 42550 by Cheyboy last updated on 27/Aug/18
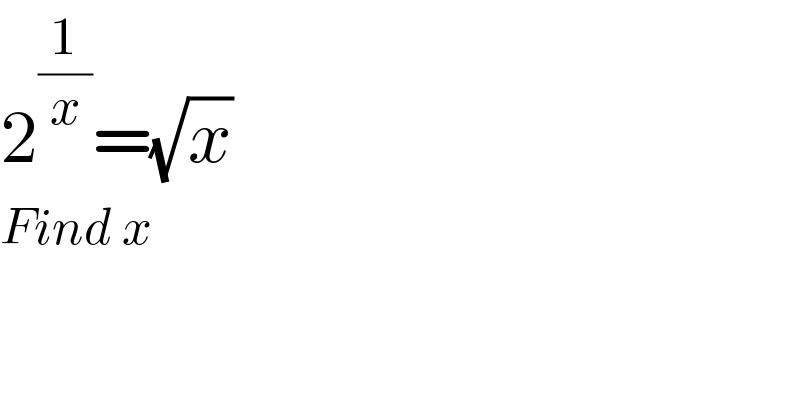
$$\mathrm{2}^{\frac{\mathrm{1}}{{x}}} =\sqrt{{x}} \\ $$$${Find}\:{x} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Aug/18
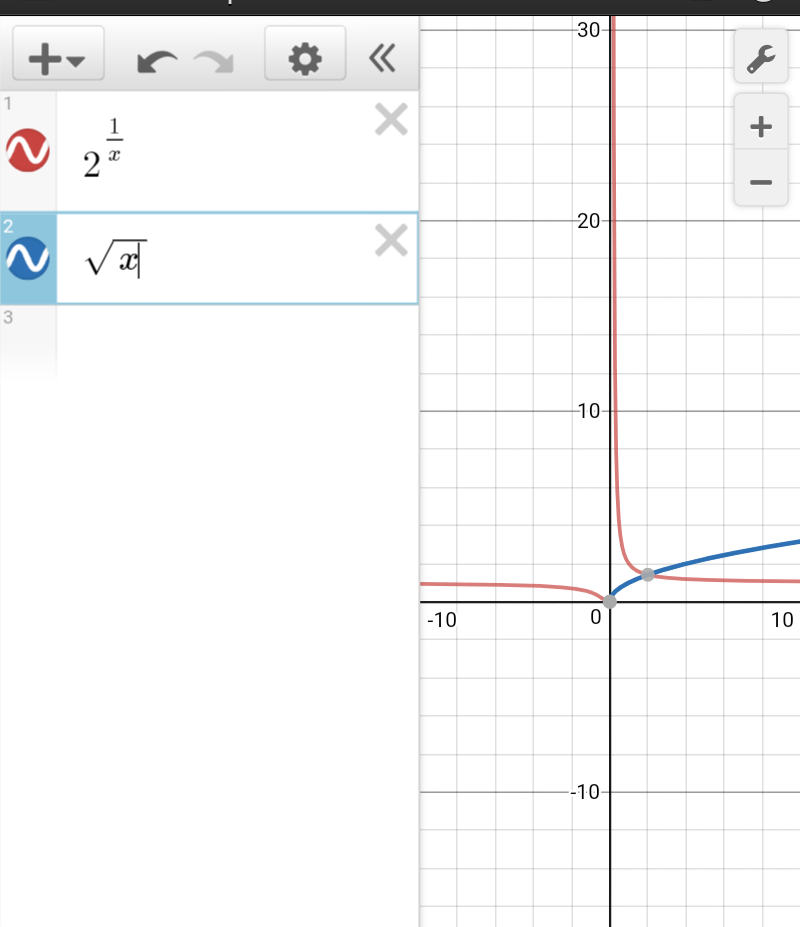
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Aug/18
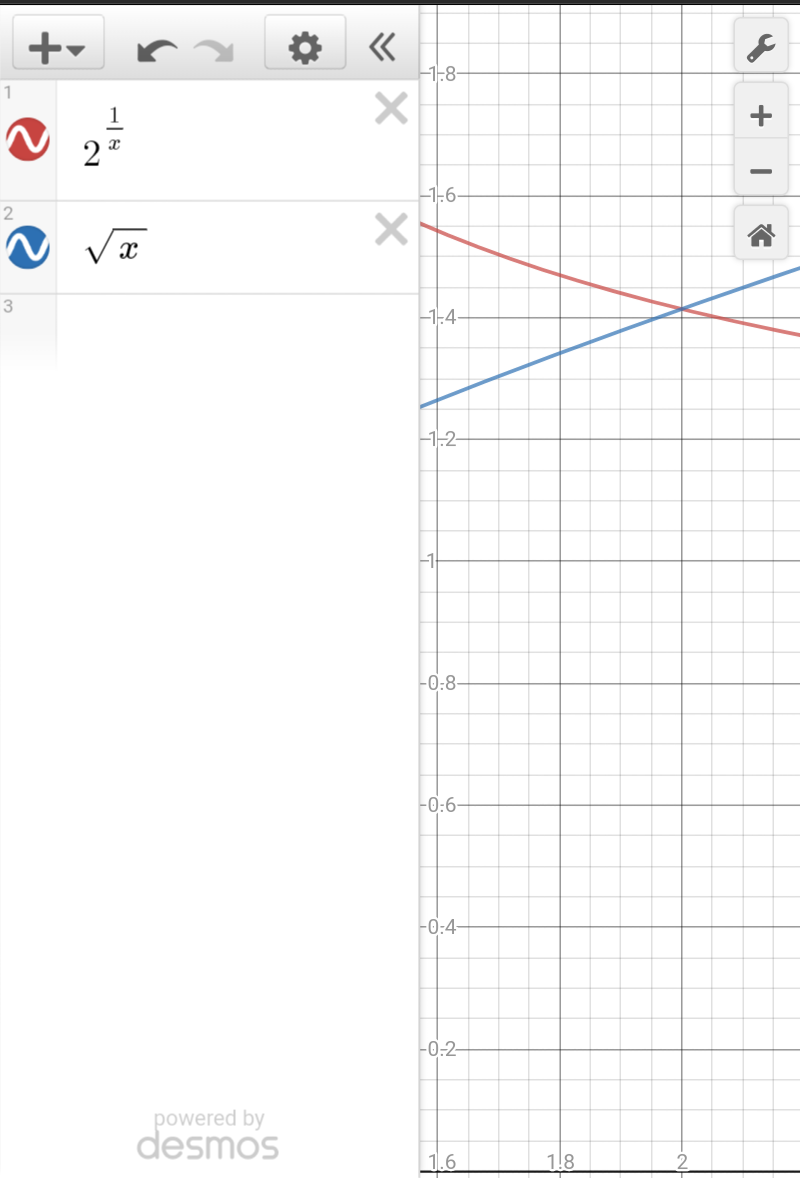
Commented by tanmay.chaudhury50@gmail.com last updated on 28/Aug/18

$${x}=\mathrm{2} \\ $$
Answered by MrW3 last updated on 28/Aug/18
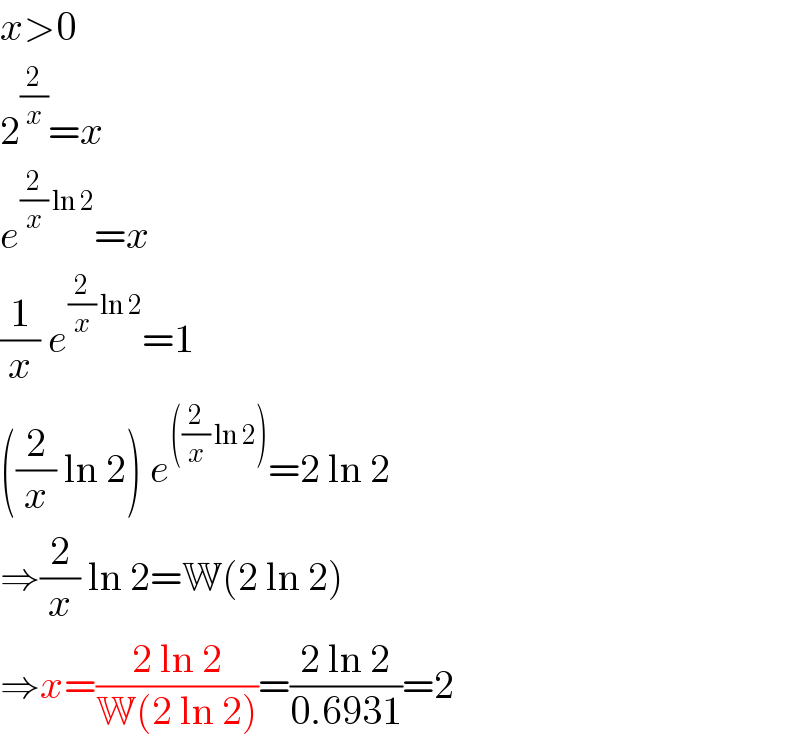
$${x}>\mathrm{0} \\ $$$$\mathrm{2}^{\frac{\mathrm{2}}{{x}}} ={x} \\ $$$${e}^{\frac{\mathrm{2}}{{x}}\:\mathrm{ln}\:\mathrm{2}} ={x} \\ $$$$\frac{\mathrm{1}}{{x}}\:{e}^{\frac{\mathrm{2}}{{x}}\:\mathrm{ln}\:\mathrm{2}} =\mathrm{1} \\ $$$$\left(\frac{\mathrm{2}}{{x}}\:\mathrm{ln}\:\mathrm{2}\right)\:{e}^{\left(\frac{\mathrm{2}}{{x}}\:\mathrm{ln}\:\mathrm{2}\right)} =\mathrm{2}\:\mathrm{ln}\:\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{2}}{{x}}\:\mathrm{ln}\:\mathrm{2}=\mathbb{W}\left(\mathrm{2}\:\mathrm{ln}\:\mathrm{2}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\:\mathrm{ln}\:\mathrm{2}}{\mathbb{W}\left(\mathrm{2}\:\mathrm{ln}\:\mathrm{2}\right)}=\frac{\mathrm{2}\:\mathrm{ln}\:\mathrm{2}}{\mathrm{0}.\mathrm{6931}}=\mathrm{2} \\ $$
