Menu Close

Question-42580

Tinku Tara 0 Comments
Pin




Question Number 42580 by Raj Singh last updated on 28/Aug/18
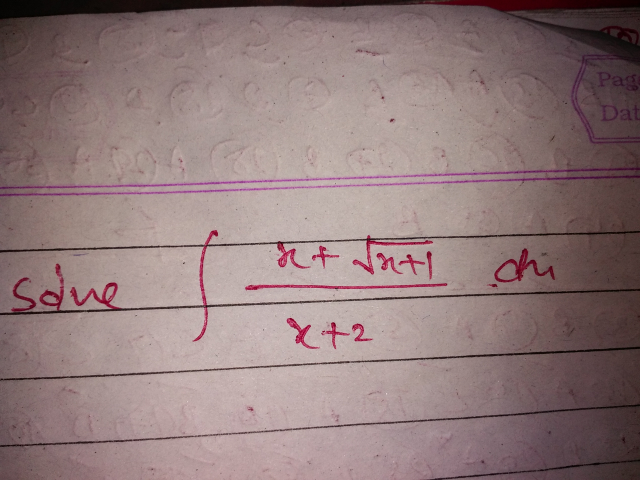
Commented by maxmathsup by imad last updated on 28/Aug/18
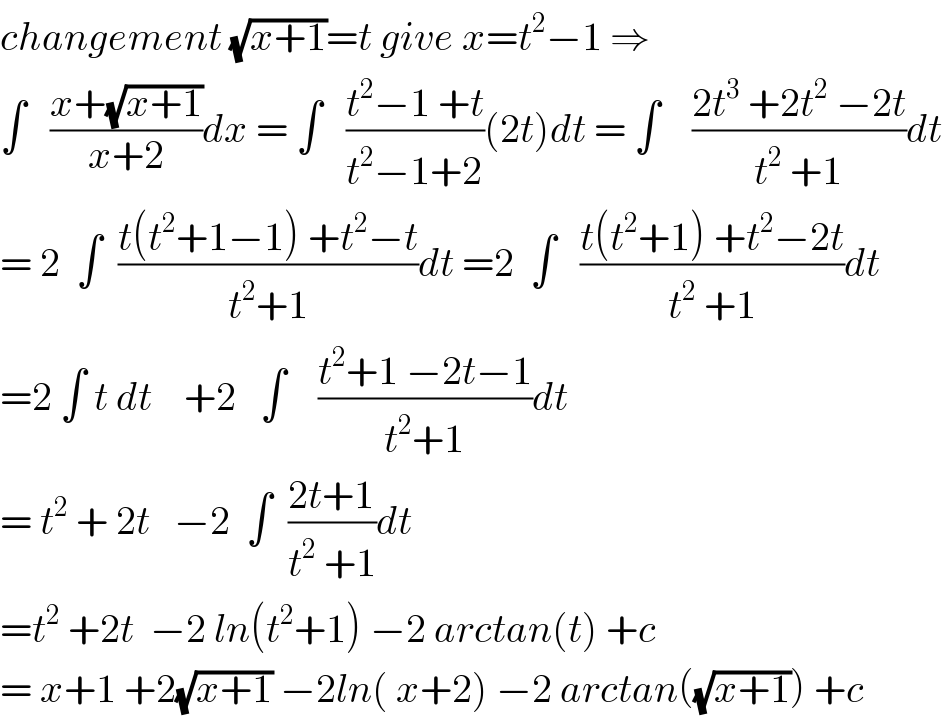
changement (√(x+1))=t give x=t^2 −1 ⇒ ∫ ((x+(√(x+1)))/(x+2))dx = ∫ ((t^2 −1 +t)/(t^2 −1+2))(2t)dt = ∫ ((2t^3 +2t^2 −2t)/(t^2 +1))dt = 2 ∫ ((t(t^2 +1−1) +t^2 −t)/(t^2 +1))dt =2 ∫ ((t(t^2 +1) +t^2 −2t)/(t^2 +1))dt =2 ∫ t dt +2 ∫ ((t^2 +1 −2t−1)/(t^2 +1))dt = t^2 + 2t −2 ∫ ((2t+1)/(t^2 +1))dt =t^2 +2t −2 ln(t^2 +1) −2 arctan(t) +c = x+1 +2(√(x+1)) −2ln( x+2) −2 arctan((√(x+1))) +c
$${changement}\:\sqrt{{x}+\mathrm{1}}={t}\:{give}\:{x}={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow \\ $$$$\int\:\:\:\frac{{x}+\sqrt{{x}+\mathrm{1}}}{{x}+\mathrm{2}}{dx}\:=\:\int\:\:\:\frac{{t}^{\mathrm{2}} −\mathrm{1}\:+{t}}{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}}\left(\mathrm{2}{t}\right){dt}\:=\:\int\:\:\:\:\frac{\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:−\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\:\mathrm{2}\:\:\int\:\:\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right)\:+{t}^{\mathrm{2}} −{t}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}\:=\mathrm{2}\:\:\int\:\:\:\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+{t}^{\mathrm{2}} −\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int\:{t}\:{dt}\:\:\:\:+\mathrm{2}\:\:\:\int\:\:\:\:\frac{{t}^{\mathrm{2}} +\mathrm{1}\:−\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$=\:{t}^{\mathrm{2}} \:+\:\mathrm{2}{t}\:\:\:−\mathrm{2}\:\:\int\:\:\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$={t}^{\mathrm{2}} \:+\mathrm{2}{t}\:\:−\mathrm{2}\:{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:−\mathrm{2}\:{arctan}\left({t}\right)\:+{c} \\ $$$$=\:{x}+\mathrm{1}\:+\mathrm{2}\sqrt{{x}+\mathrm{1}}\:−\mathrm{2}{ln}\left(\:{x}+\mathrm{2}\right)\:−\mathrm{2}\:{arctan}\left(\sqrt{{x}+\mathrm{1}}\right)\:+{c} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Aug/18
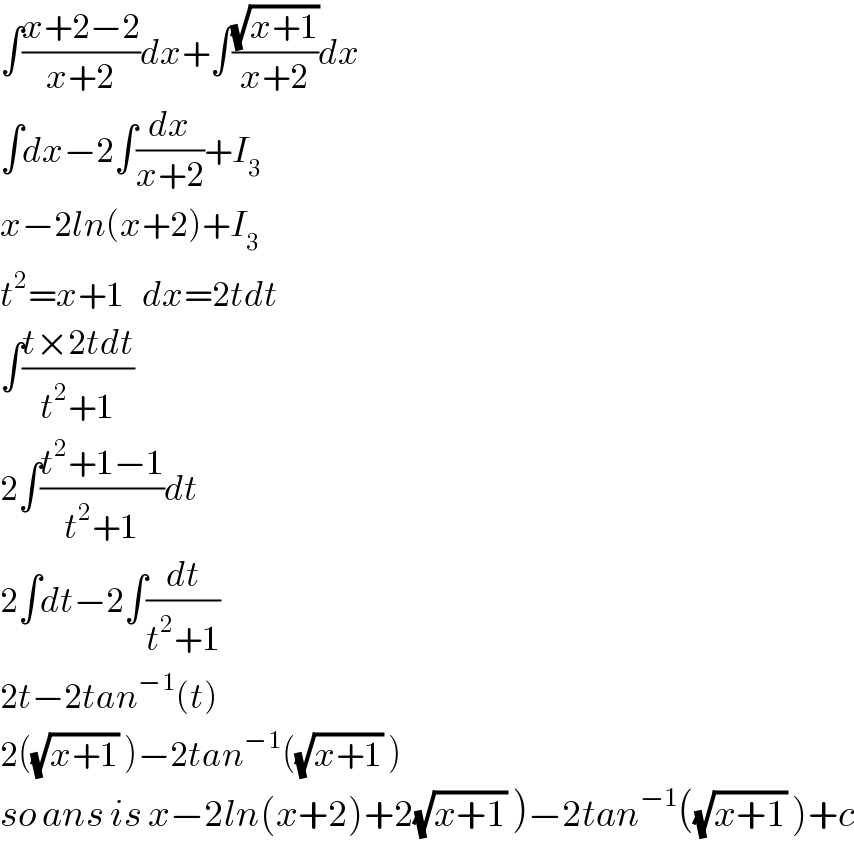
∫((x+2−2)/(x+2))dx+∫((√(x+1))/(x+2))dx ∫dx−2∫(dx/(x+2))+I_3 x−2ln(x+2)+I_3 t^2 =x+1 dx=2tdt ∫((t×2tdt)/(t^2 +1)) 2∫((t^2 +1−1)/(t^2 +1))dt 2∫dt−2∫(dt/(t^2 +1)) 2t−2tan^(−1) (t) 2((√(x+1)) )−2tan^(−1) ((√(x+1)) ) so ans is x−2ln(x+2)+2(√(x+1)) )−2tan^(−1) ((√(x+1)) )+c
$$\int\frac{{x}+\mathrm{2}−\mathrm{2}}{{x}+\mathrm{2}}{dx}+\int\frac{\sqrt{{x}+\mathrm{1}}}{{x}+\mathrm{2}}{dx} \\ $$$$\int{dx}−\mathrm{2}\int\frac{{dx}}{{x}+\mathrm{2}}+{I}_{\mathrm{3}} \\ $$$${x}−\mathrm{2}{ln}\left({x}+\mathrm{2}\right)+{I}_{\mathrm{3}} \\ $$$${t}^{\mathrm{2}} ={x}+\mathrm{1}\:\:\:{dx}=\mathrm{2}{tdt} \\ $$$$\int\frac{{t}×\mathrm{2}{tdt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{2}\int\frac{{t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$\mathrm{2}\int{dt}−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{2}{t}−\mathrm{2}{tan}^{−\mathrm{1}} \left({t}\right) \\ $$$$\mathrm{2}\left(\sqrt{{x}+\mathrm{1}}\:\right)−\mathrm{2}{tan}^{−\mathrm{1}} \left(\sqrt{{x}+\mathrm{1}}\:\right) \\ $$$$\left.{so}\:{ans}\:{is}\:{x}−\mathrm{2}{ln}\left({x}+\mathrm{2}\right)+\mathrm{2}\sqrt{{x}+\mathrm{1}}\:\right)−\mathrm{2}{tan}^{−\mathrm{1}} \left(\sqrt{{x}+\mathrm{1}}\:\right)+{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *