Question Number 108143 by abony1303 last updated on 15/Aug/20

$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{sin}^{\mathrm{2}} \mathrm{3x} \\ $$$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$\mathrm{Please}\:\mathrm{help}\:\mathrm{ASAP} \\ $$
Answered by ajfour last updated on 15/Aug/20
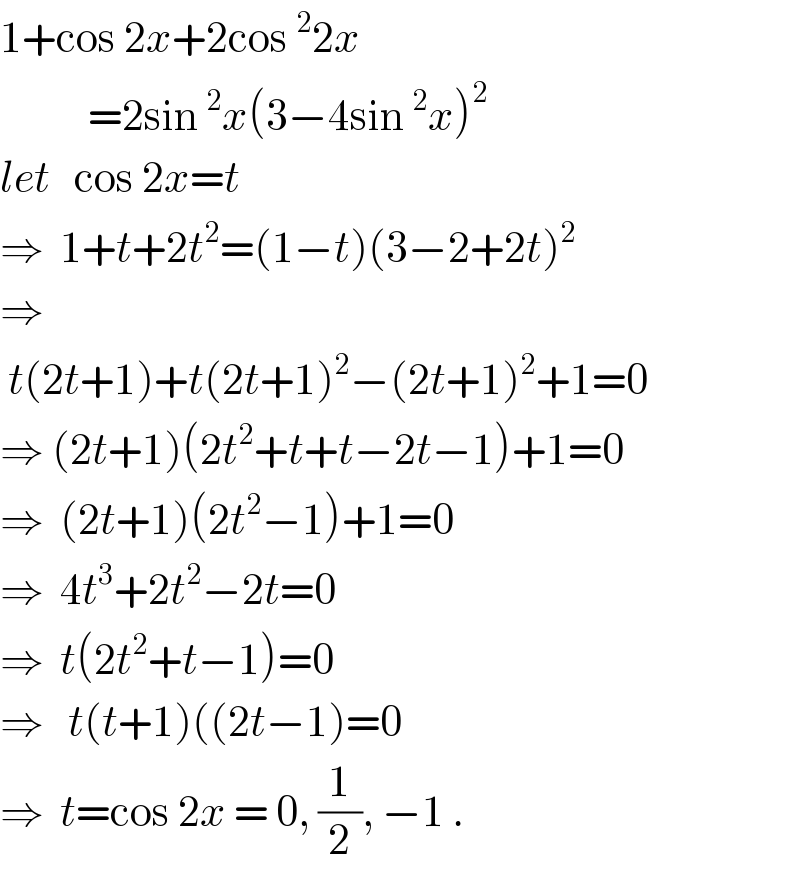
$$\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}+\mathrm{2cos}\:^{\mathrm{2}} \mathrm{2}{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2sin}\:^{\mathrm{2}} {x}\left(\mathrm{3}−\mathrm{4sin}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} \\ $$$${let}\:\:\:\mathrm{cos}\:\mathrm{2}{x}={t} \\ $$$$\Rightarrow\:\:\mathrm{1}+{t}+\mathrm{2}{t}^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)\left(\mathrm{3}−\mathrm{2}+\mathrm{2}{t}\right)^{\mathrm{2}} \:\: \\ $$$$\Rightarrow \\ $$$$\:{t}\left(\mathrm{2}{t}+\mathrm{1}\right)+{t}\left(\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{2}{t}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{2}{t}+\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} +{t}+{t}−\mathrm{2}{t}−\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\left(\mathrm{2}{t}+\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}\right)+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{4}{t}^{\mathrm{3}} +\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{t}=\mathrm{0} \\ $$$$\Rightarrow\:\:{t}\left(\mathrm{2}{t}^{\mathrm{2}} +{t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{t}\left({t}+\mathrm{1}\right)\left(\left(\mathrm{2}{t}−\mathrm{1}\right)=\mathrm{0}\right. \\ $$$$\Rightarrow\:\:{t}=\mathrm{cos}\:\mathrm{2}{x}\:=\:\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{2}},\:−\mathrm{1}\:. \\ $$
Answered by 1549442205PVT last updated on 15/Aug/20
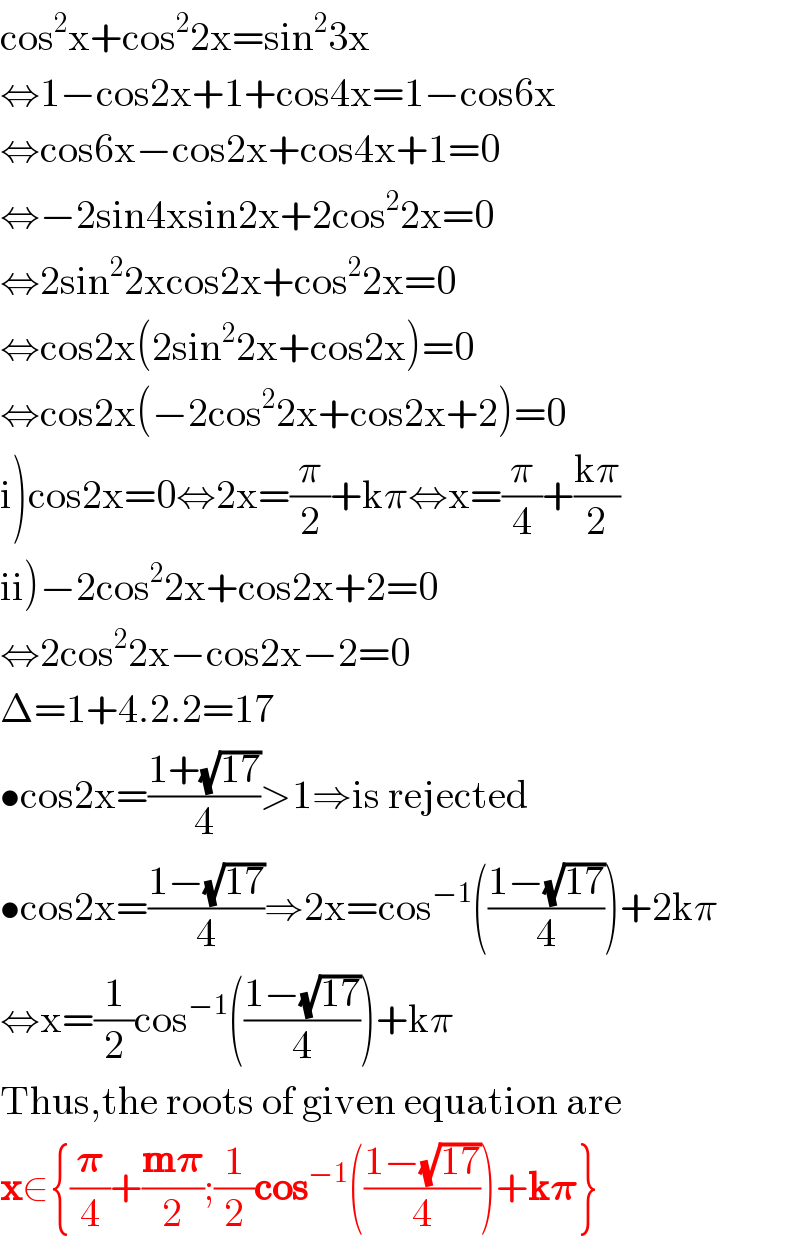
$$\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{sin}^{\mathrm{2}} \mathrm{3x} \\ $$$$\Leftrightarrow\mathrm{1}−\mathrm{cos2x}+\mathrm{1}+\mathrm{cos4x}=\mathrm{1}−\mathrm{cos6x} \\ $$$$\Leftrightarrow\mathrm{cos6x}−\mathrm{cos2x}+\mathrm{cos4x}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow−\mathrm{2sin4xsin2x}+\mathrm{2cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2sin}^{\mathrm{2}} \mathrm{2xcos2x}+\mathrm{cos}^{\mathrm{2}} \mathrm{2x}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{cos2x}\left(\mathrm{2sin}^{\mathrm{2}} \mathrm{2x}+\mathrm{cos2x}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{cos2x}\left(−\mathrm{2cos}^{\mathrm{2}} \mathrm{2x}+\mathrm{cos2x}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\left.\mathrm{i}\right)\mathrm{cos2x}=\mathrm{0}\Leftrightarrow\mathrm{2x}=\frac{\pi}{\mathrm{2}}+\mathrm{k}\pi\Leftrightarrow\mathrm{x}=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{k}\pi}{\mathrm{2}} \\ $$$$\left.\mathrm{ii}\right)−\mathrm{2cos}^{\mathrm{2}} \mathrm{2x}+\mathrm{cos2x}+\mathrm{2}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2cos}^{\mathrm{2}} \mathrm{2x}−\mathrm{cos2x}−\mathrm{2}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}+\mathrm{4}.\mathrm{2}.\mathrm{2}=\mathrm{17} \\ $$$$\bullet\mathrm{cos2x}=\frac{\mathrm{1}+\sqrt{\mathrm{17}}}{\mathrm{4}}>\mathrm{1}\Rightarrow\mathrm{is}\:\mathrm{rejected} \\ $$$$\bullet\mathrm{cos2x}=\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{4}}\Rightarrow\mathrm{2x}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{4}}\right)+\mathrm{2k}\pi \\ $$$$\Leftrightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{4}}\right)+\mathrm{k}\pi \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{are} \\ $$$$\boldsymbol{\mathrm{x}}\in\left\{\frac{\boldsymbol{\pi}}{\mathrm{4}}+\frac{\boldsymbol{\mathrm{m}\pi}}{\mathrm{2}};\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{cos}}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{17}}}{\mathrm{4}}\right)+\boldsymbol{\mathrm{k}\pi}\right\} \\ $$
