Question Number 42670 by Tawa1 last updated on 31/Aug/18

$$\mathrm{If}\:\:\mathrm{a},\:\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\:\mathrm{are}\:\mathrm{in}\:\mathrm{a}\:\mathrm{GP}.\:\:\mathrm{Prove}\:\mathrm{that}\:\:\:\mathrm{log}_{\mathrm{n}} \mathrm{a}\:,\:\:\mathrm{log}_{\mathrm{n}} \mathrm{b}\:\:,\:\:\mathrm{log}_{\mathrm{n}} \mathrm{c}\:\:\:\mathrm{are}\:\mathrm{in}\:\mathrm{AP} \\ $$
Commented by maxmathsup by imad last updated on 31/Aug/18
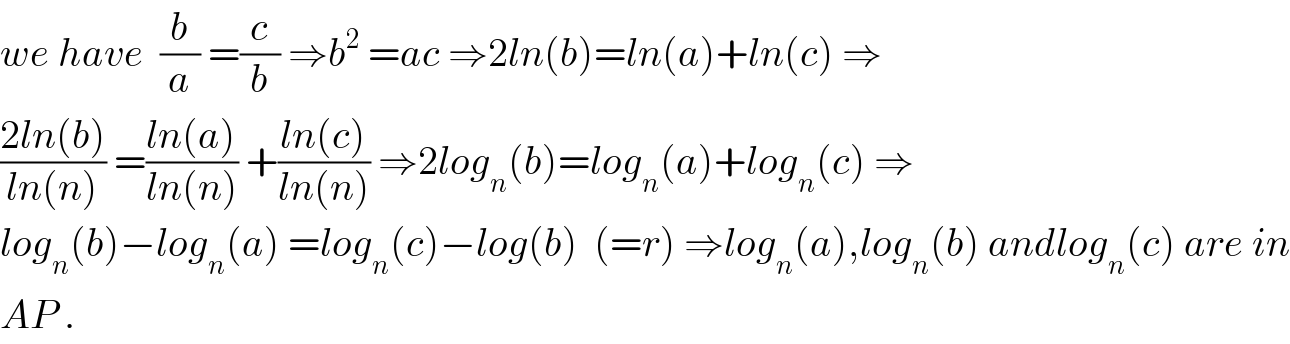
$${we}\:{have}\:\:\frac{{b}}{{a}}\:=\frac{{c}}{{b}}\:\Rightarrow{b}^{\mathrm{2}} \:={ac}\:\Rightarrow\mathrm{2}{ln}\left({b}\right)={ln}\left({a}\right)+{ln}\left({c}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{2}{ln}\left({b}\right)}{{ln}\left({n}\right)}\:=\frac{{ln}\left({a}\right)}{{ln}\left({n}\right)}\:+\frac{{ln}\left({c}\right)}{{ln}\left({n}\right)}\:\Rightarrow\mathrm{2}{log}_{{n}} \left({b}\right)={log}_{{n}} \left({a}\right)+{log}_{{n}} \left({c}\right)\:\Rightarrow \\ $$$${log}_{{n}} \left({b}\right)−{log}_{{n}} \left({a}\right)\:={log}_{{n}} \left({c}\right)−{log}\left({b}\right)\:\:\left(={r}\right)\:\Rightarrow{log}_{{n}} \left({a}\right),{log}_{{n}} \left({b}\right)\:{andlog}_{{n}} \left({c}\right)\:{are}\:{in} \\ $$$${AP}\:. \\ $$
Commented by Tawa1 last updated on 31/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by prof Abdo imad last updated on 31/Aug/18

$${thank}\:{you}\:{sir}. \\ $$
Answered by Rio Michael last updated on 31/Aug/18
![a,b,c in GP b^2 = ac taking log_n on both sides log_n b^2 = log_n ac 2log_n b = log_n a + log_n c log_n b= ((log_n a + log_n c)/2) which is the Arithmetic mean(AM) [b = ((a+c)/2)] for A.Ps](https://www.tinkutara.com/question/Q42677.png)
$$\:{a},{b},{c}\:{in}\:{GP} \\ $$$${b}^{\mathrm{2}} =\:{ac} \\ $$$${taking}\:\:{log}_{{n}} \:{on}\:{both}\:{sides} \\ $$$${log}_{{n}} {b}^{\mathrm{2}} \:=\:{log}_{{n}} {ac} \\ $$$$\mathrm{2}{log}_{{n}} {b}\:=\:{log}_{{n}} {a}\:+\:{log}_{{n}} {c} \\ $$$${log}_{{n}} {b}=\:\frac{{log}_{{n}} {a}\:+\:{log}_{{n}} {c}}{\mathrm{2}} \\ $$$${which}\:{is}\:{the}\:{Arithmetic}\:{mean}\left({AM}\right)\:\left[{b}\:=\:\frac{{a}+{c}}{\mathrm{2}}\right]\:{for}\:{A}.{Ps} \\ $$
Commented by Tawa1 last updated on 31/Aug/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Rio Michael last updated on 31/Aug/18

$${welcome} \\ $$
