Question Number 108450 by bemath last updated on 17/Aug/20
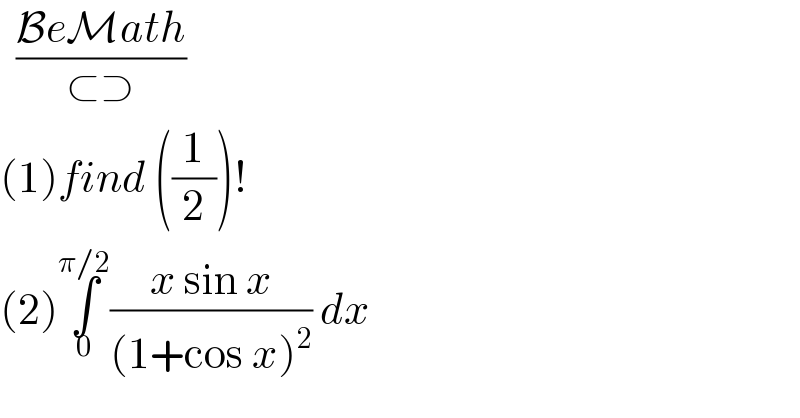
$$\:\:\frac{\mathcal{B}{e}\mathcal{M}{ath}}{\subset\supset} \\ $$$$\left(\mathrm{1}\right){find}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)! \\ $$$$\left(\mathrm{2}\right)\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{x}\:\mathrm{sin}\:{x}}{\left(\mathrm{1}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx} \\ $$
Commented by Smail last updated on 17/Aug/20

$${I}_{{n}} =\int_{\mathrm{0}} ^{\infty} {t}^{{n}} {e}^{−{t}} {dt}={n}! \\ $$$${n}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${I}_{\mathrm{1}/\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} \sqrt{{t}}{e}^{−{t}} {dt}=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)! \\ $$$${x}=\sqrt{{t}}\Rightarrow{dx}=\frac{{dt}}{\mathrm{2}\sqrt{{t}}} \\ $$$${I}_{\mathrm{1}/\mathrm{2}} =\mathrm{2}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}^{\mathrm{2}} } {dx}=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)! \\ $$$${By}\:{parts} \\ $$$${u}={x}\Rightarrow{u}'=\mathrm{1} \\ $$$${v}'={xe}^{−{x}^{\mathrm{2}} } \Rightarrow{v}=\frac{−\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } \\ $$$${I}_{\mathrm{1}/\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)! \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$${So} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$
Commented by bemath last updated on 17/Aug/20

$${thank}\:{you} \\ $$
Answered by john santu last updated on 17/Aug/20

Answered by Dwaipayan Shikari last updated on 17/Aug/20
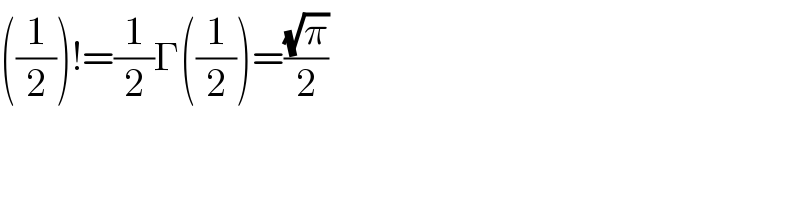
$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$
