Question Number 359 by 123456 last updated on 25/Jan/15
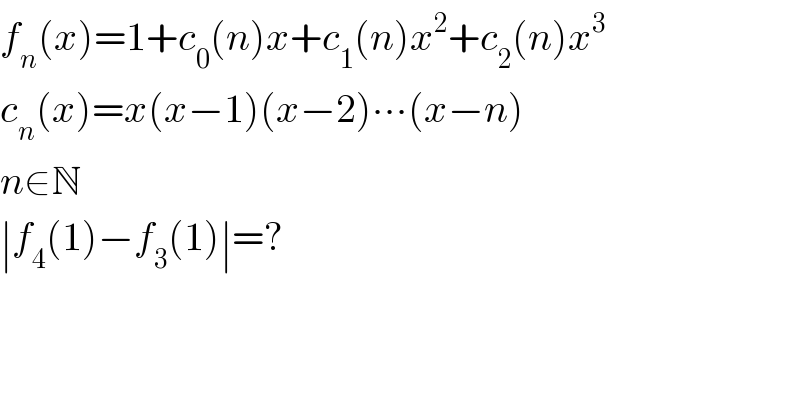
$${f}_{{n}} \left({x}\right)=\mathrm{1}+{c}_{\mathrm{0}} \left({n}\right){x}+{c}_{\mathrm{1}} \left({n}\right){x}^{\mathrm{2}} +{c}_{\mathrm{2}} \left({n}\right){x}^{\mathrm{3}} \\ $$$${c}_{{n}} \left({x}\right)={x}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)\centerdot\centerdot\centerdot\left({x}−{n}\right) \\ $$$${n}\in\mathbb{N} \\ $$$$\mid{f}_{\mathrm{4}} \left(\mathrm{1}\right)−{f}_{\mathrm{3}} \left(\mathrm{1}\right)\mid=? \\ $$
Answered by prakash jain last updated on 24/Dec/14
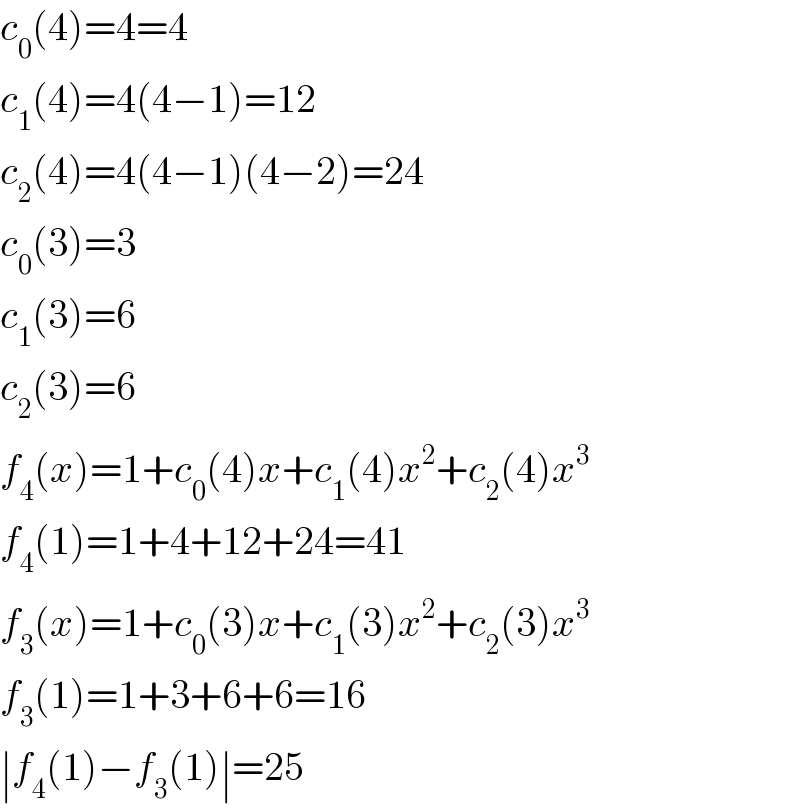
$${c}_{\mathrm{0}} \left(\mathrm{4}\right)=\mathrm{4}=\mathrm{4} \\ $$$${c}_{\mathrm{1}} \left(\mathrm{4}\right)=\mathrm{4}\left(\mathrm{4}−\mathrm{1}\right)=\mathrm{12} \\ $$$${c}_{\mathrm{2}} \left(\mathrm{4}\right)=\mathrm{4}\left(\mathrm{4}−\mathrm{1}\right)\left(\mathrm{4}−\mathrm{2}\right)=\mathrm{24} \\ $$$${c}_{\mathrm{0}} \left(\mathrm{3}\right)=\mathrm{3} \\ $$$${c}_{\mathrm{1}} \left(\mathrm{3}\right)=\mathrm{6} \\ $$$${c}_{\mathrm{2}} \left(\mathrm{3}\right)=\mathrm{6} \\ $$$${f}_{\mathrm{4}} \left({x}\right)=\mathrm{1}+{c}_{\mathrm{0}} \left(\mathrm{4}\right){x}+{c}_{\mathrm{1}} \left(\mathrm{4}\right){x}^{\mathrm{2}} +{c}_{\mathrm{2}} \left(\mathrm{4}\right){x}^{\mathrm{3}} \\ $$$${f}_{\mathrm{4}} \left(\mathrm{1}\right)=\mathrm{1}+\mathrm{4}+\mathrm{12}+\mathrm{24}=\mathrm{41} \\ $$$${f}_{\mathrm{3}} \left({x}\right)=\mathrm{1}+{c}_{\mathrm{0}} \left(\mathrm{3}\right){x}+{c}_{\mathrm{1}} \left(\mathrm{3}\right){x}^{\mathrm{2}} +{c}_{\mathrm{2}} \left(\mathrm{3}\right){x}^{\mathrm{3}} \\ $$$${f}_{\mathrm{3}} \left(\mathrm{1}\right)=\mathrm{1}+\mathrm{3}+\mathrm{6}+\mathrm{6}=\mathrm{16} \\ $$$$\mid{f}_{\mathrm{4}} \left(\mathrm{1}\right)−{f}_{\mathrm{3}} \left(\mathrm{1}\right)\mid=\mathrm{25} \\ $$
