Question-108502

Question Number 108502 by mnjuly1970 last updated on 17/Aug/20

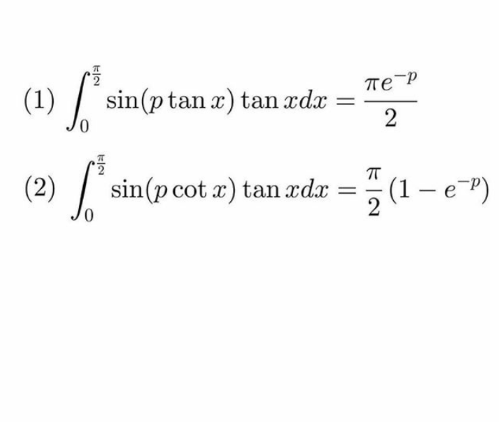
Commented by mnjuly1970 last updated on 17/Aug/20

$$\clubsuit{please}\:{prove}\:\:{above}\:{integrals} \\ $$$${equalities}.\clubsuit \\ $$

Answered by mathmax by abdo last updated on 17/Aug/20

1) A_p =∫_0 ^(π/2) sin(ptanx)tanx dx changement tanx =t give A_p =∫_0 ^∞ sin(pt)t (dt/(1+t^2 )) =∫_0 ^∞ ((tsin(pt))/(1+t^2 )) dt =(1/2)∫_(−∞) ^(+∞) ((tsin(pt))/(t^2 +1))dt =(1/2)Im(∫_(−∞) ^(+∞ ) ((te^(ipt) )/(t^2 +1))dt) let ϕ(z) =((z e^(ipz) )/(z^2 +1)) ⇒ϕ(z) =((z e^(ipz) )/((z−i)(z+i))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπRes(ϕ,i) =2iπ .((i e^(−p) )/(2i)) =iπ e^(−p) ⇒ ★A_p =(π/2)e^(−p) ★

$$\left.\mathrm{1}\right)\:\:\mathrm{A}_{\mathrm{p}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}\left(\mathrm{ptanx}\right)\mathrm{tanx}\:\mathrm{dx}\:\:\mathrm{changement}\:\:\mathrm{tanx}\:=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}_{\mathrm{p}} =\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\left(\mathrm{pt}\right)\mathrm{t}\:\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{tsin}\left(\mathrm{pt}\right)}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{tsin}\left(\mathrm{pt}\right)}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Im}\left(\int_{−\infty} ^{+\infty\:} \:\frac{\mathrm{te}^{\mathrm{ipt}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\right)\:\:\mathrm{let} \\ $$$$\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}\:\mathrm{e}^{\mathrm{ipz}} }{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}\:\mathrm{e}^{\mathrm{ipz}} }{\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{2i}\pi\:\:.\frac{\mathrm{i}\:\mathrm{e}^{−\mathrm{p}} }{\mathrm{2i}}\:=\mathrm{i}\pi\:\mathrm{e}^{−\mathrm{p}} \:\Rightarrow \\ $$$$\bigstar\mathrm{A}_{\mathrm{p}} =\frac{\pi}{\mathrm{2}}\mathrm{e}^{−\mathrm{p}} \:\bigstar \\ $$

Commented by mnjuly1970 last updated on 17/Aug/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$

Commented by mathmax by abdo last updated on 17/Aug/20

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Commented by mnjuly1970 last updated on 17/Aug/20

the god bless you and keep you my friend and my masster ..(thank you)^∞

$$\mathrm{the}\:\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{and}\:\mathrm{keep}\:\mathrm{you}\:\mathrm{my} \\ $$$$\mathrm{friend}\:\mathrm{and}\:\mathrm{my}\:\mathrm{masster}\:..\left(\mathrm{thank}\:\mathrm{you}\right)^{\infty} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply