Menu Close

The-sixth-term-of-an-A-P-is-2-its-common-difference-is-greater-than-one-Find-the-value-of-the-common-difference-so-that-the-product-of-the-first-fourth-and-fifth-terms-is-the-greatest-

Tinku Tara 0 Comments
Pin




Question Number 108854 by ZiYangLee last updated on 19/Aug/20
The sixth term of an A.P. is 2, its common difference is greater than one. Find the value of the common difference so that the product of the first, fourth and fifth terms is the greatest.
$$\mathrm{The}\:\mathrm{sixth}\:\mathrm{term}\:\mathrm{of}\:\mathrm{an}\:\mathrm{A}.\mathrm{P}.\:\mathrm{is}\:\mathrm{2},\:\mathrm{its} \\ $$$$\mathrm{common}\:\mathrm{difference}\:\mathrm{is}\:\mathrm{greater}\:\mathrm{than} \\ $$$$\mathrm{one}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{common} \\ $$$$\mathrm{difference}\:\mathrm{so}\:\mathrm{that}\:\mathrm{the}\:\mathrm{product}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{first},\:\mathrm{fourth}\:\mathrm{and}\:\mathrm{fifth}\:\mathrm{terms}\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{greatest}. \\ $$
Answered by $@y@m last updated on 20/Aug/20
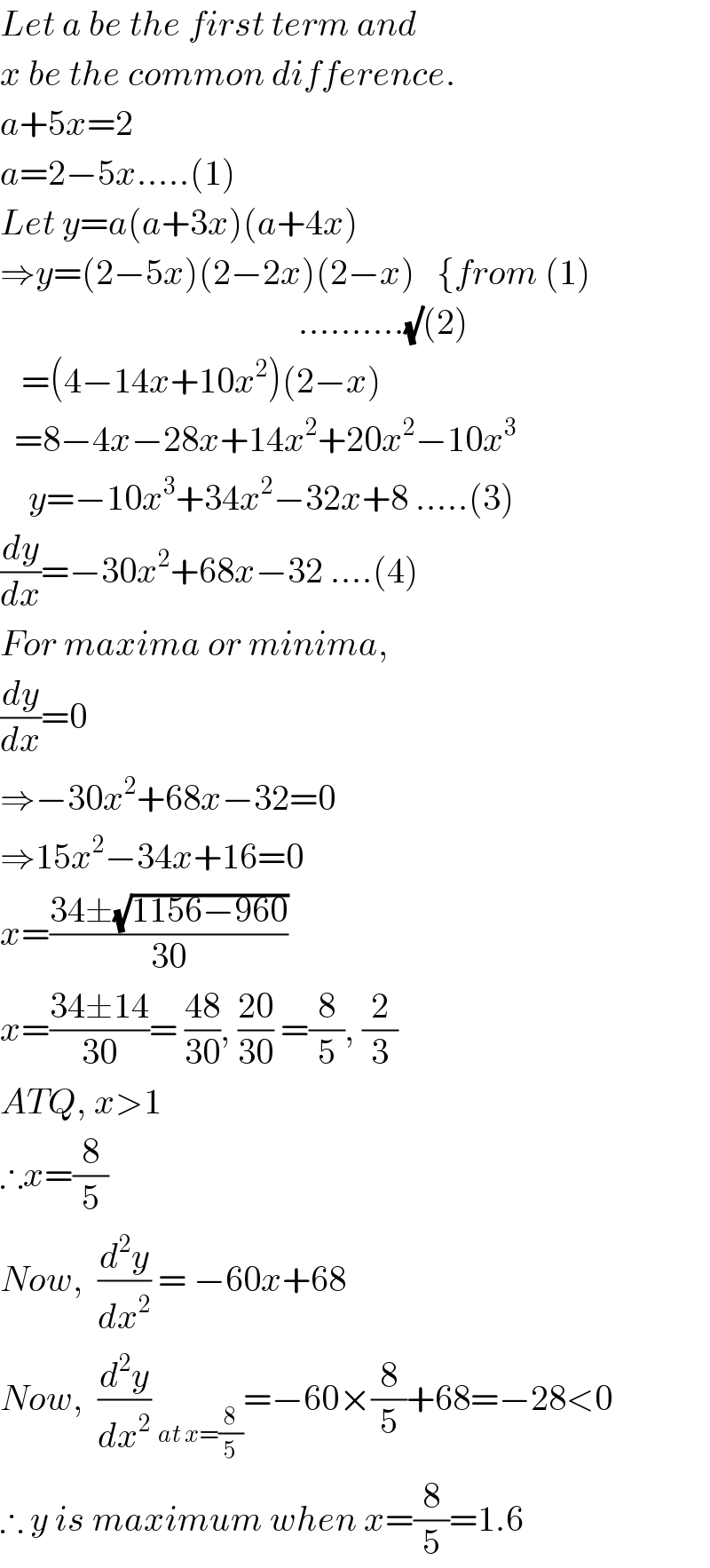
Let a be the first term and x be the common difference. a+5x=2 a=2−5x.....(1) Let y=a(a+3x)(a+4x) ⇒y=(2−5x)(2−2x)(2−x) {from (1) ..........(√)(2) =(4−14x+10x^2 )(2−x) =8−4x−28x+14x^2 +20x^2 −10x^3 y=−10x^3 +34x^2 −32x+8 .....(3) (dy/dx)=−30x^2 +68x−32 ....(4) For maxima or minima, (dy/dx)=0 ⇒−30x^2 +68x−32=0 ⇒15x^2 −34x+16=0 x=((34±(√(1156−960)))/(30)) x=((34±14)/(30))= ((48)/(30)), ((20)/(30)) =(8/5), (2/3) ATQ, x>1 ∴x=(8/5) Now, (d^2 y/dx^2 ) = −60x+68 Now, (d^2 y/dx^2 ) _(at x=(8/5)) =−60×(8/5)+68=−28<0 ∴ y is maximum when x=(8/5)=1.6
$${Let}\:{a}\:{be}\:{the}\:{first}\:{term}\:{and}\: \\ $$$${x}\:{be}\:{the}\:{common}\:{difference}. \\ $$$${a}+\mathrm{5}{x}=\mathrm{2} \\ $$$${a}=\mathrm{2}−\mathrm{5}{x}…..\left(\mathrm{1}\right) \\ $$$${Let}\:{y}={a}\left({a}+\mathrm{3}{x}\right)\left({a}+\mathrm{4}{x}\right) \\ $$$$\Rightarrow{y}=\left(\mathrm{2}−\mathrm{5}{x}\right)\left(\mathrm{2}−\mathrm{2}{x}\right)\left(\mathrm{2}−{x}\right)\:\:\:\left\{{from}\:\left(\mathrm{1}\right)\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……….\sqrt{}\left(\mathrm{2}\right) \\ $$$$\:\:\:=\left(\mathrm{4}−\mathrm{14}{x}+\mathrm{10}{x}^{\mathrm{2}} \right)\left(\mathrm{2}−{x}\right) \\ $$$$\:\:=\mathrm{8}−\mathrm{4}{x}−\mathrm{28}{x}+\mathrm{14}{x}^{\mathrm{2}} +\mathrm{20}{x}^{\mathrm{2}} −\mathrm{10}{x}^{\mathrm{3}} \\ $$$$\:\:\:\:{y}=−\mathrm{10}{x}^{\mathrm{3}} +\mathrm{34}{x}^{\mathrm{2}} −\mathrm{32}{x}+\mathrm{8}\:…..\left(\mathrm{3}\right) \\ $$$$\frac{{dy}}{{dx}}=−\mathrm{30}{x}^{\mathrm{2}} +\mathrm{68}{x}−\mathrm{32}\:….\left(\mathrm{4}\right) \\ $$$${For}\:{maxima}\:{or}\:{minima}, \\ $$$$\frac{{dy}}{{dx}}=\mathrm{0} \\ $$$$\Rightarrow−\mathrm{30}{x}^{\mathrm{2}} +\mathrm{68}{x}−\mathrm{32}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{15}{x}^{\mathrm{2}} −\mathrm{34}{x}+\mathrm{16}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{34}\pm\sqrt{\mathrm{1156}−\mathrm{960}}}{\mathrm{30}} \\ $$$${x}=\frac{\mathrm{34}\pm\mathrm{14}}{\mathrm{30}}=\:\frac{\mathrm{48}}{\mathrm{30}},\:\frac{\mathrm{20}}{\mathrm{30}}\:=\frac{\mathrm{8}}{\mathrm{5}},\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${ATQ},\:{x}>\mathrm{1} \\ $$$$\therefore{x}=\frac{\mathrm{8}}{\mathrm{5}} \\ $$$${Now},\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:−\mathrm{60}{x}+\mathrm{68} \\ $$$${Now},\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:_{{at}\:{x}=\frac{\mathrm{8}}{\mathrm{5}}} =−\mathrm{60}×\frac{\mathrm{8}}{\mathrm{5}}+\mathrm{68}=−\mathrm{28}<\mathrm{0} \\ $$$$\therefore\:{y}\:{is}\:{maximum}\:{when}\:{x}=\frac{\mathrm{8}}{\mathrm{5}}=\mathrm{1}.\mathrm{6} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *