Question Number 43343 by pieroo last updated on 10/Sep/18
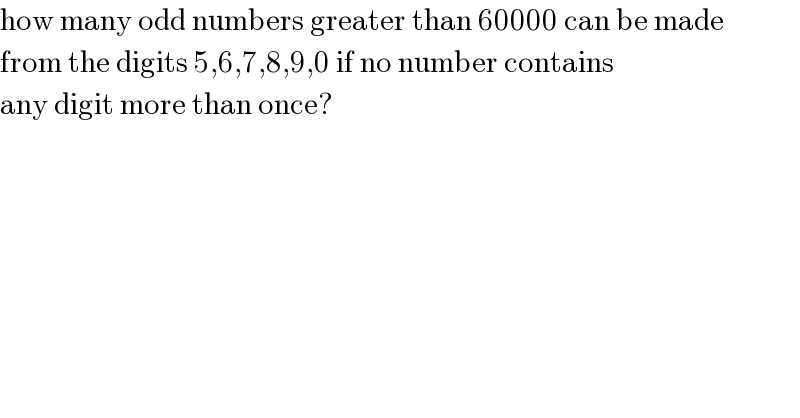
$$\mathrm{how}\:\mathrm{many}\:\mathrm{odd}\:\mathrm{numbers}\:\mathrm{greater}\:\mathrm{than}\:\mathrm{60000}\:\mathrm{can}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{digits}\:\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0}\:\mathrm{if}\:\mathrm{no}\:\mathrm{number}\:\mathrm{contains} \\ $$$$\mathrm{any}\:\mathrm{digit}\:\mathrm{more}\:\mathrm{than}\:\mathrm{once}? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 10/Sep/18

$$\underset{\mathrm{5}} {−}\:\underset{\mathrm{4}} {−}\:\underset{\mathrm{3}} {−}\:\underset{\mathrm{2}} {−}\:\underset{\mathrm{1}} {−}\: \\ $$$${digits}\:{are}\:\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0}\:\:\left({six}\:{nos}\:{of}\:{digit}\right) \\ $$$${numbers}\:{greater}\:{than}\:\mathrm{60},\mathrm{000}… \\ $$$${the}\:\mathrm{5}{th}\:{place}\:{can}\:{be}\:{filled}\:{by}\:\left(\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9}\right) \\ $$$${numbers}\:{are}\:{odd}\:{so}\:\mathrm{1}{st}\:{place}\:{can}\:{be}\:{filled}\left(\mathrm{5},\mathrm{7},\mathrm{9}\right) \\ $$$$\left.\mathrm{1}\right)\underset{\mathrm{5}} {\overset{\mathrm{6}} {−}}\:\underset{\mathrm{4}} {−}\:\underset{\mathrm{3}} {−}\:\underset{\mathrm{2}} {−}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {−}}\:\mathrm{5}{th}\:{place}\:{filled}\:{by}\:\mathrm{6}\:{and}\:\mathrm{1}{st}\:{place}\:{by}\mathrm{5} \\ $$$$\mathrm{4}{th}\:{place}\:{can}\:{be}\:{filled}\:{by}\:{any}\:{digit}\:{out}\:{of}\left(\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0}\right) \\ $$$${so}\:\mathrm{4}{ways} \\ $$$$\mathrm{3}{rd}\:{place}\:{can}\:{be}\:{filled}\:{by}\:{any}\:{remaining}\:{three}\:{digit} \\ $$$${so}\:\mathrm{3}{ways} \\ $$$$\mathrm{2}{nd}\:{place}\:{can}\:{be}\:{filled}\:{by}\:{any}\:{remaining}\:{two} \\ $$$${digit}\:{so}\:\mathrm{2}\:{ways} \\ $$$$\mathcal{T}{hus}\:{the}\:{numbers}\:{whose}\:\mathrm{1}{st}\:{place}\:{is}\:\mathrm{5} \\ $$$${and}\:\mathrm{5}{th}\:{place}\:{is}\:\mathrm{6}\:\:{that}\:{means}\:{greater}\:{than} \\ $$$$\mathrm{60000}\:{but}\:{odd}\:{are}\:\mathrm{4}×\mathrm{3}×\mathrm{2}=\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{6}} {−}}\:\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {−}}\:\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{6}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{7}} {−}}\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{6}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{9}} {−}}−\mathrm{24} \\ $$$${thus}\:\mathrm{24}×\mathrm{3}=\mathrm{72} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {−}}\:\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{7}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{9}} {−}}\:\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{8}} {−}}\overset{} {\:}\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {−}}\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{8}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{7}} {−}}\rightarrow\mathrm{24} \\ $$$$\:\underset{\mathrm{5}} {\overset{\mathrm{8}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{9}} {−}}\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{9}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\:\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{5}} {−}}\rightarrow\mathrm{24} \\ $$$$\underset{\mathrm{5}} {\overset{\mathrm{9}} {−}}\:\underset{\mathrm{4}} {\overset{×} {−}}\underset{\mathrm{3}} {\overset{×} {−}}\:\underset{\mathrm{2}} {\overset{×} {−}}\:\underset{\mathrm{1}} {\overset{\mathrm{7}} {−}}\rightarrow\mathrm{24} \\ $$$$\mathrm{5}{th}\:{place}\:\mathrm{6}\:\rightarrow\mathrm{24}×\mathrm{3}=\mathrm{72} \\ $$$$\mathrm{5}{th}\:{placd}\:\mathrm{7}\rightarrow\mathrm{24}×\mathrm{2}=\mathrm{48} \\ $$$$\mathrm{5}{th}\:{place}\:\mathrm{8}\rightarrow\mathrm{24}×\mathrm{3}=\mathrm{72} \\ $$$$\mathrm{5}{th}\:{place}\:\mathrm{9}\rightarrow\mathrm{24}×\mathrm{2}=\mathrm{48} \\ $$$${total}=\mathrm{72}+\mathrm{48}+\mathrm{72}+\mathrm{48}=\mathrm{240} \\ $$$$ \\ $$$$ \\ $$$$\:\:\:\:\: \\ $$
