Question Number 109016 by mathdave last updated on 20/Aug/20
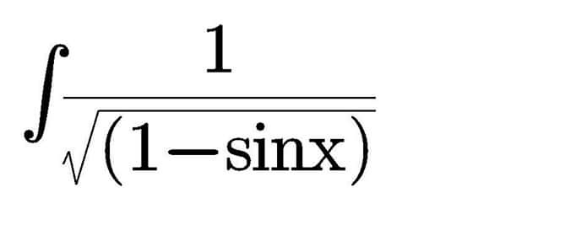
Answered by Dwaipayan Shikari last updated on 20/Aug/20

$$\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{sinx}}}{dx} \\ $$$$\int\frac{\mathrm{1}}{{cos}\frac{{x}}{\mathrm{2}}−{sin}\frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{1}}{{cos}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int{sec}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right){dx} \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}\int{secudu}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}={u}\:\:,\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:=\frac{{du}}{{dx}}\right. \\ $$$$\sqrt{\mathrm{2}}{log}\left({secu}+{tanu}\right)+{C} \\ $$$$\sqrt{\mathrm{2}}\:{log}\left({sec}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)+{tan}\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right)\right)+{C} \\ $$
Commented by $@y@m last updated on 20/Aug/20

$${Wonderful}! \\ $$
Answered by mathmax by abdo last updated on 20/Aug/20
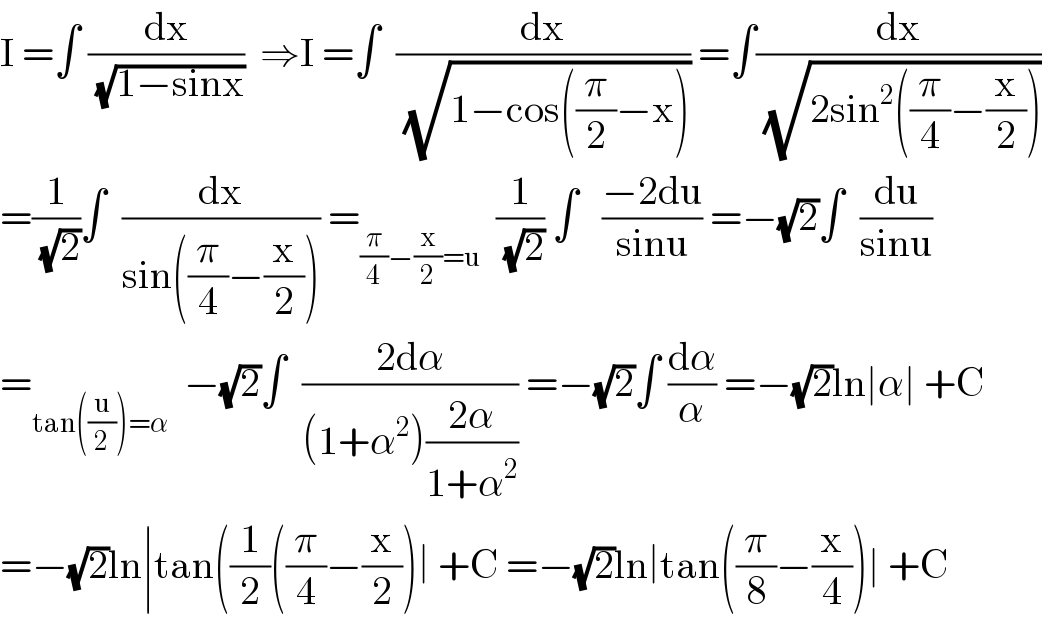
$$\mathrm{I}\:=\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{sinx}}}\:\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{x}\right)}}\:=\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\:\:\frac{\mathrm{dx}}{\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)}\:=_{\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{u}} \:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\:\:\frac{−\mathrm{2du}}{\mathrm{sinu}}\:=−\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{du}}{\mathrm{sinu}} \\ $$$$=_{\mathrm{tan}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)=\alpha} \:\:−\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{2d}\alpha}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)\frac{\mathrm{2}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }}\:=−\sqrt{\mathrm{2}}\int\:\frac{\mathrm{d}\alpha}{\alpha}\:=−\sqrt{\mathrm{2}}\mathrm{ln}\mid\alpha\mid\:+\mathrm{C} \\ $$$$=−\sqrt{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{4}}−\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\:+\mathrm{C}\:=−\sqrt{\mathrm{2}}\mathrm{ln}\mid\mathrm{tan}\left(\frac{\pi}{\mathrm{8}}−\frac{\mathrm{x}}{\mathrm{4}}\right)\mid\:+\mathrm{C}\right. \\ $$
