Question Number 174556 by mnjuly1970 last updated on 04/Aug/22
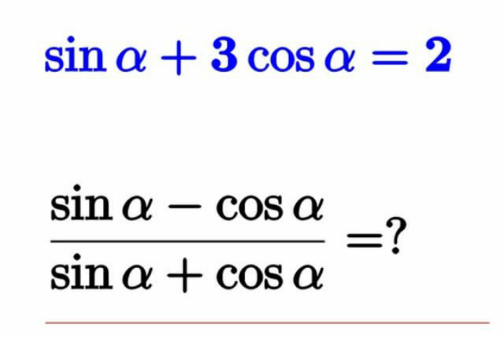
Commented by infinityaction last updated on 04/Aug/22

$$\:\:\:\:\:\:\:\mathrm{tan}\alpha\:+\mathrm{3}\:=\:\mathrm{2sec}\alpha \\ $$$$\:\:\:\:\:\:\mathrm{3tan}^{\mathrm{2}} \alpha\:−\mathrm{6tan}\alpha\:−\mathrm{5}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{tan}\alpha\:\:=\:\:\:\frac{\mathrm{6}\:\pm\:\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{6}}\:\:\:=\:\:\frac{\mathrm{sin}\alpha\:}{\mathrm{cos}\alpha\:}\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{sin}\alpha−\mathrm{cos}\alpha\:\:}{\mathrm{sin}\alpha+\mathrm{cos}\alpha\:\:}\:\:=\:\:\frac{\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{12}+\mathrm{4}\sqrt{\mathrm{6}}}\:=\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}} \\ $$$${or}\:\:\:\:\frac{\mathrm{sin}\alpha\:−\:\mathrm{cos}\alpha\:}{\mathrm{sin}\alpha\:+\mathrm{cos}\alpha\:\:}\:\:=\:\:\frac{−\mathrm{4}\sqrt{\mathrm{6}}}{\mathrm{12}−\mathrm{4}\sqrt{\mathrm{6}}}\:=\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\sqrt{\mathrm{3}}} \\ $$
Answered by cortano1 last updated on 04/Aug/22

$$\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \alpha}\:=\:\mathrm{2}−\mathrm{3cos}\:\alpha \\ $$$$\:\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \alpha=\mathrm{4}−\mathrm{12cos}\:\alpha+\mathrm{9cos}\:^{\mathrm{2}} \alpha \\ $$$$\:\mathrm{10cos}\:^{\mathrm{2}} \alpha−\mathrm{12cos}\:\alpha+\mathrm{3}=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{cos}\:\alpha=\frac{\mathrm{6}+\sqrt{\mathrm{6}}}{\mathrm{10}}\Rightarrow\mathrm{sin}\:\alpha=\mathrm{2}−\left(\frac{\mathrm{18}+\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{10}}\right)=\frac{\mathrm{2}−\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{10}}}\\{\mathrm{cos}\:\alpha=\frac{\mathrm{6}−\sqrt{\mathrm{6}}}{\mathrm{10}}\Rightarrow\mathrm{sin}\:\alpha=\mathrm{2}−\left(\frac{\mathrm{18}−\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{10}}\right)=\frac{\mathrm{2}+\mathrm{3}\sqrt{\mathrm{6}}}{\mathrm{10}}}\end{cases} \\ $$$$\:\frac{\mathrm{sin}\:\alpha−\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha+\mathrm{cos}\:\alpha}\:=\:\frac{\mathrm{2}−\mathrm{3}\sqrt{\mathrm{6}}−\mathrm{6}−\sqrt{\mathrm{6}}}{\mathrm{2}−\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{6}+\sqrt{\mathrm{6}}}=\frac{−\mathrm{4}\sqrt{\mathrm{6}}−\mathrm{4}}{\mathrm{8}−\mathrm{2}\sqrt{\mathrm{6}}} \\ $$$$\:\:=\:\frac{\mathrm{2}\sqrt{\mathrm{6}}+\mathrm{2}}{\:\sqrt{\mathrm{6}}−\mathrm{4}}\:{or}\:\frac{\mathrm{2}+\mathrm{3}\sqrt{\mathrm{6}}−\mathrm{6}+\sqrt{\mathrm{6}}}{\mathrm{2}+\mathrm{3}\sqrt{\mathrm{6}}+\mathrm{6}−\sqrt{\mathrm{6}}}=\frac{\mathrm{4}\sqrt{\mathrm{6}}−\mathrm{4}}{\mathrm{8}+\mathrm{2}\sqrt{\mathrm{6}}}=\frac{\mathrm{2}\sqrt{\mathrm{6}}−\mathrm{2}}{\mathrm{4}+\sqrt{\mathrm{6}}} \\ $$
Answered by MJS_new last updated on 04/Aug/22

$$\alpha=\mathrm{2arctan}\:{t}\:\Rightarrow\:\mathrm{sin}\:\alpha\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\wedge\mathrm{cos}\:\alpha\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{3}{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2} \\ $$$${t}^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{5}}{t}−\frac{\mathrm{1}}{\mathrm{5}}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{5}}\pm\frac{\sqrt{\mathrm{6}}}{\mathrm{5}} \\ $$$$−\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}=−\mathrm{2}\pm\sqrt{\mathrm{6}} \\ $$
Commented by infinityaction last updated on 04/Aug/22
$${nice}\:{solution}\:{sir} \\ $$
