Question Number 109029 by nimnim last updated on 20/Aug/20
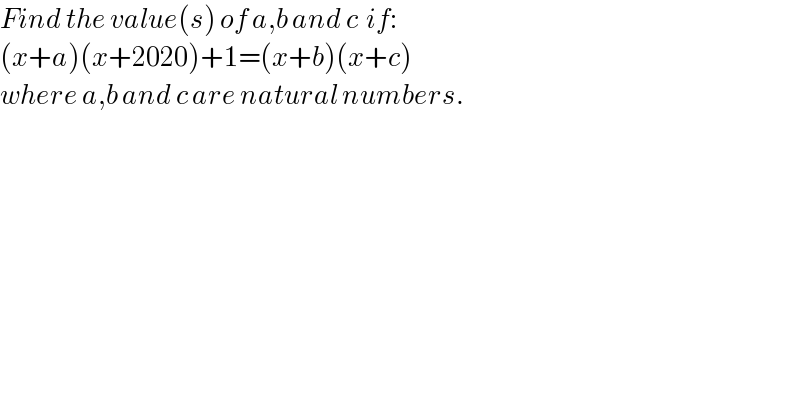
$${Find}\:{the}\:{value}\left({s}\right)\:{of}\:{a},{b}\:{and}\:{c}\:\:{if}: \\ $$$$\left({x}+{a}\right)\left({x}+\mathrm{2020}\right)+\mathrm{1}=\left({x}+{b}\right)\left({x}+{c}\right) \\ $$$${where}\:{a},{b}\:{and}\:{c}\:{are}\:{natural}\:{numbers}. \\ $$
Answered by floor(10²Eta[1]) last updated on 21/Aug/20

$$\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2020}+\mathrm{a}\right)\mathrm{x}+\mathrm{2020a}+\mathrm{1}=\mathrm{x}^{\mathrm{2}} +\left(\mathrm{b}+\mathrm{c}\right)\mathrm{x}+\mathrm{bc} \\ $$$$\Rightarrow\mathrm{2020}+\mathrm{a}=\mathrm{b}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{2020a}+\mathrm{1}=\mathrm{bc} \\ $$$$\mathrm{a}=\mathrm{b}+\mathrm{c}−\mathrm{2020} \\ $$$$\mathrm{2020}\left(\mathrm{b}+\mathrm{c}−\mathrm{2020}\right)+\mathrm{1}=\mathrm{bc} \\ $$$$\mathrm{2020b}+\mathrm{2020c}−\mathrm{2020}^{\mathrm{2}} +\mathrm{1}=\mathrm{bc} \\ $$$$\mathrm{bc}−\mathrm{2020b}−\mathrm{2020c}+\mathrm{2020}^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{b}−\mathrm{2020}\right)\left(\mathrm{c}−\mathrm{2020}\right)=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{only}\:\mathrm{ways}\:\mathrm{we}\:\mathrm{can}\:\mathrm{factor}\:\mathrm{1}\:\mathrm{are} \\ $$$$\mathrm{1}.\mathrm{1}\:\mathrm{or}\:\left(−\mathrm{1}\right)\left(−\mathrm{1}\right) \\ $$$$\mathrm{I}\:\mathrm{case}: \\ $$$$\mathrm{b}−\mathrm{2020}=\mathrm{1}=\mathrm{c}−\mathrm{2020} \\ $$$$\Rightarrow\mathrm{b}=\mathrm{c}=\mathrm{2021}\therefore\mathrm{a}=\mathrm{2022} \\ $$$$\mathrm{II}\:\mathrm{case}: \\ $$$$\mathrm{b}−\mathrm{2020}=−\mathrm{1}=\mathrm{c}−\mathrm{2020} \\ $$$$\Rightarrow\mathrm{b}=\mathrm{c}=\mathrm{2019}\therefore\mathrm{a}=\mathrm{2018} \\ $$$$ \\ $$$$\mathrm{so}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{a},\:\mathrm{b},\:\mathrm{c}\:\mathrm{are}: \\ $$$$\left(\mathrm{2022},\:\mathrm{2021},\:\mathrm{2021}\right),\:\left(\mathrm{2018},\:\mathrm{2019},\:\mathrm{2019}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 22/Aug/20
$$\underset{\mathrm{W}} {\overset{\mathrm{W}} {\mathrm{O}}}\:\underset{!} {\overset{!} {!}},\:{great}!…\mathcal{T}{hanks}\:{floor}\:\mathcal{S}{ir}! \\ $$
