Question Number 109068 by n0y0n last updated on 20/Aug/20
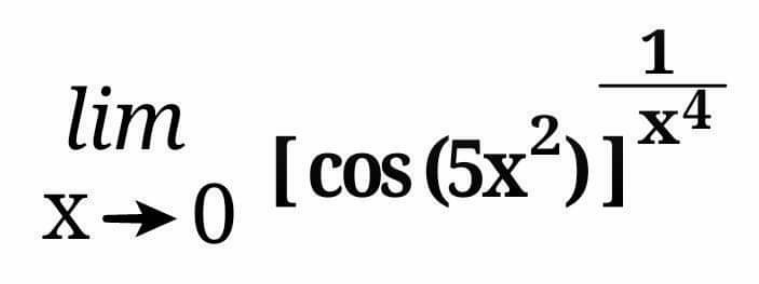
Answered by Dwaipayan Shikari last updated on 20/Aug/20
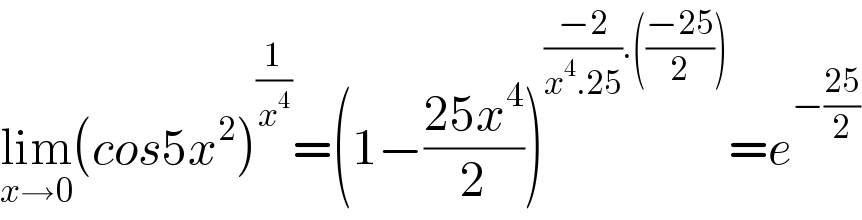
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({cos}\mathrm{5}{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{{x}^{\mathrm{4}} }} =\left(\mathrm{1}−\frac{\mathrm{25}{x}^{\mathrm{4}} }{\mathrm{2}}\right)^{\frac{−\mathrm{2}}{{x}^{\mathrm{4}} .\mathrm{25}}.\left(\frac{−\mathrm{25}}{\mathrm{2}}\right)} ={e}^{−\frac{\mathrm{25}}{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 20/Aug/20
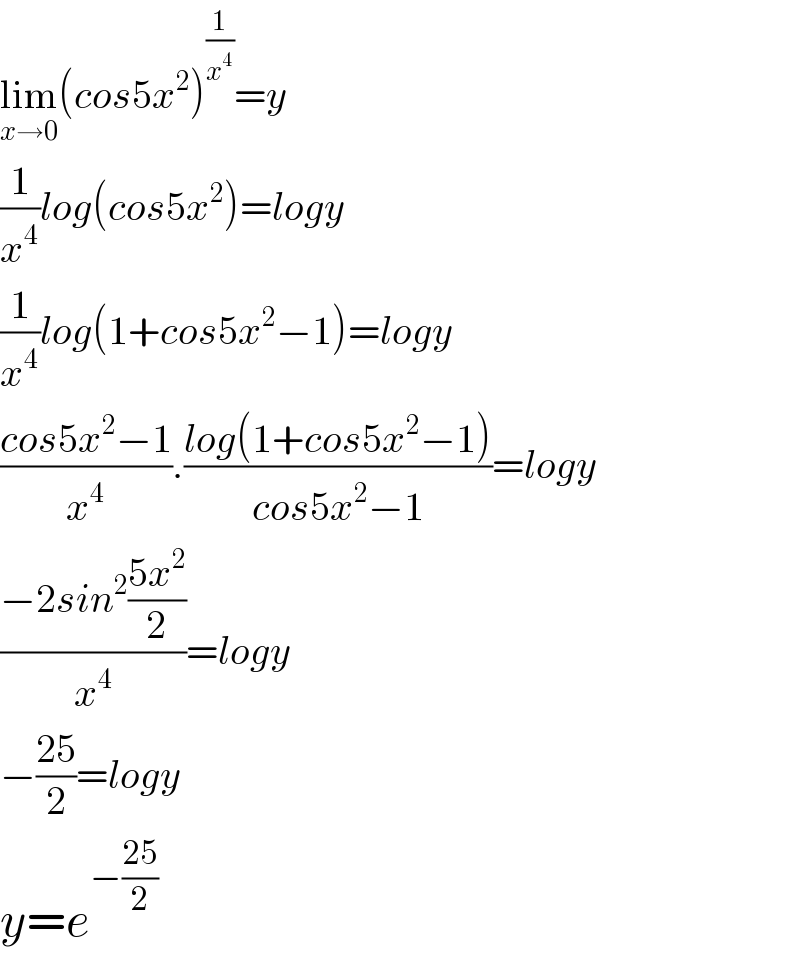
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({cos}\mathrm{5}{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{{x}^{\mathrm{4}} }} ={y} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} }{log}\left({cos}\mathrm{5}{x}^{\mathrm{2}} \right)={logy} \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} }{log}\left(\mathrm{1}+{cos}\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}\right)={logy} \\ $$$$\frac{{cos}\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} }.\frac{{log}\left(\mathrm{1}+{cos}\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}\right)}{{cos}\mathrm{5}{x}^{\mathrm{2}} −\mathrm{1}}={logy} \\ $$$$\frac{−\mathrm{2}{sin}^{\mathrm{2}} \frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{2}}}{{x}^{\mathrm{4}} }={logy} \\ $$$$−\frac{\mathrm{25}}{\mathrm{2}}={logy} \\ $$$${y}={e}^{−\frac{\mathrm{25}}{\mathrm{2}}} \\ $$
