Question Number 43549 by peter frank last updated on 11/Sep/18
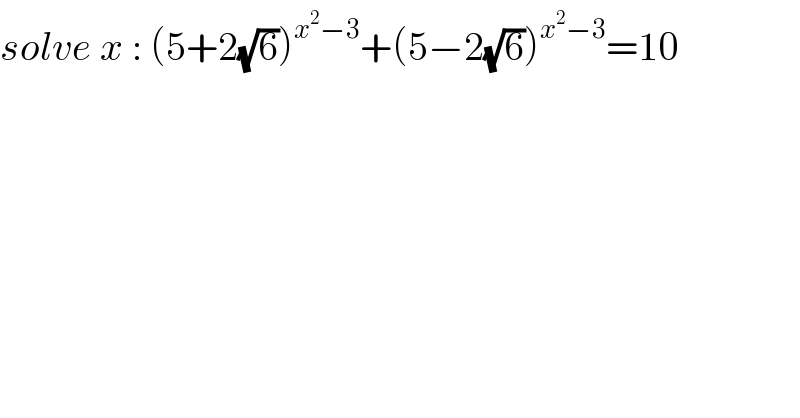
$${solve}\:{x}\::\:\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{{x}^{\mathrm{2}} −\mathrm{3}} +\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{{x}^{\mathrm{2}} −\mathrm{3}} =\mathrm{10} \\ $$
Commented by Cheyboy last updated on 12/Sep/18
![(5+2(√6))(5−2(√6)) = 1 [(5+2(√6))(5−2(√6))^ ]^(x^2 −3) =1^(x^2 −3) (5−2(√6))^(x^2 −3) = (1/((5+2(√6))^(x^2 −3) )) (5+2(√6))^(x^2 −3) +(1/((5+2(√6))^(x^2 −3) ))=10 m=(5+2(√6))^(x^2 −3) m+(1/m)=10 m^2 −10m+1=0 m= 5±2(√6) (5+2(√6))^(x^2 −3) =(5+2(√6))^1 x^2 −3 = 1 x^2 = 4 x= ±2](https://www.tinkutara.com/question/Q43563.png)
$$\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)\:=\:\mathrm{1} \\ $$$$\left[\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{} \right]^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} =\mathrm{1}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} \\ $$$$\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} =\:\frac{\mathrm{1}}{\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} } \\ $$$$\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} +\frac{\mathrm{1}}{\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} }=\mathrm{10} \\ $$$$\mathrm{m}=\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} \\ $$$$\mathrm{m}+\frac{\mathrm{1}}{\mathrm{m}}=\mathrm{10} \\ $$$$\mathrm{m}^{\mathrm{2}} −\mathrm{10m}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{m}=\:\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\:\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{x}^{\mathrm{2}} −\mathrm{3}} =\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{\mathrm{1}} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{3}\:=\:\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} =\:\mathrm{4} \\ $$$$\mathrm{x}=\:\pm\mathrm{2} \\ $$
Answered by behi83417@gmail.com last updated on 12/Sep/18
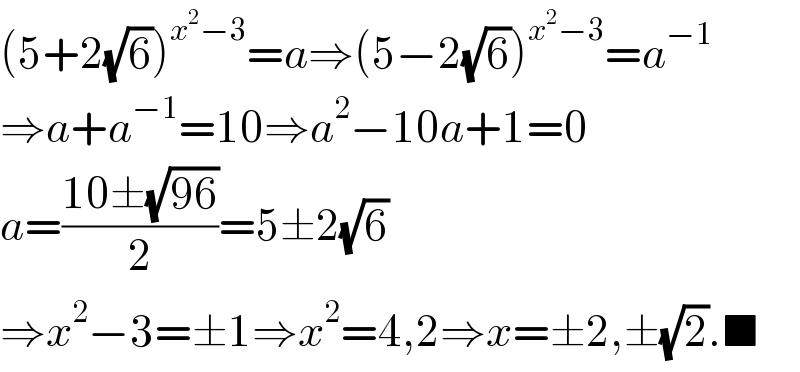
$$\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{6}}\right)^{{x}^{\mathrm{2}} −\mathrm{3}} ={a}\Rightarrow\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{6}}\right)^{{x}^{\mathrm{2}} −\mathrm{3}} ={a}^{−\mathrm{1}} \\ $$$$\Rightarrow{a}+{a}^{−\mathrm{1}} =\mathrm{10}\Rightarrow{a}^{\mathrm{2}} −\mathrm{10}{a}+\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{10}\pm\sqrt{\mathrm{96}}}{\mathrm{2}}=\mathrm{5}\pm\mathrm{2}\sqrt{\mathrm{6}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}=\pm\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{4},\mathrm{2}\Rightarrow{x}=\pm\mathrm{2},\pm\sqrt{\mathrm{2}}.\blacksquare \\ $$
Commented by peter frank last updated on 12/Sep/18

$${thank}\:{you} \\ $$
