Question Number 135419 by liberty last updated on 13/Mar/21
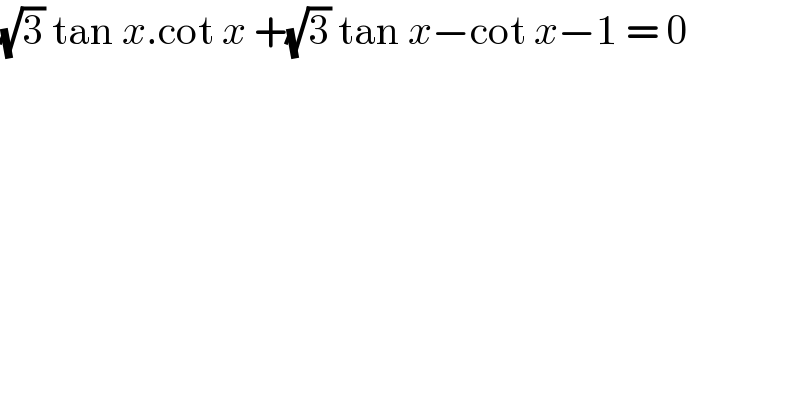
$$\sqrt{\mathrm{3}}\:\mathrm{tan}\:{x}.\mathrm{cot}\:{x}\:+\sqrt{\mathrm{3}}\:\mathrm{tan}\:{x}−\mathrm{cot}\:{x}−\mathrm{1}\:=\:\mathrm{0} \\ $$
Answered by benjo_mathlover last updated on 13/Mar/21
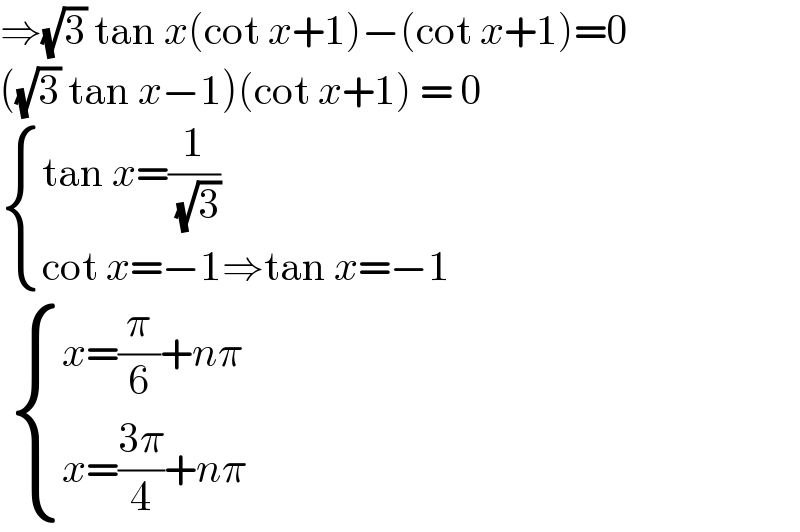
$$\Rightarrow\sqrt{\mathrm{3}}\:\mathrm{tan}\:{x}\left(\mathrm{cot}\:{x}+\mathrm{1}\right)−\left(\mathrm{cot}\:{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\sqrt{\mathrm{3}}\:\mathrm{tan}\:{x}−\mathrm{1}\right)\left(\mathrm{cot}\:{x}+\mathrm{1}\right)\:=\:\mathrm{0} \\ $$$$\begin{cases}{\mathrm{tan}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\\{\mathrm{cot}\:{x}=−\mathrm{1}\Rightarrow\mathrm{tan}\:{x}=−\mathrm{1}}\end{cases} \\ $$$$\:\begin{cases}{{x}=\frac{\pi}{\mathrm{6}}+{n}\pi}\\{{x}=\frac{\mathrm{3}\pi}{\mathrm{4}}+{n}\pi}\end{cases} \\ $$
