Question Number 174685 by mnjuly1970 last updated on 08/Aug/22

$$ \\ $$$$\:\:\:\:\:{prove}\:{that}\:: \\ $$$$\: \\ $$$$\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\:{x}^{\:\mathrm{2}} }{{cosh}\left({x}\:\right)}\:{dx}\:=\:\frac{\pi^{\:\mathrm{3}} }{\:\mathrm{8}} \\ $$$$ \\ $$
Answered by princeDera last updated on 08/Aug/22

$$ \\ $$$$ \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{co}{sh}\left({x}\right)}\:=\:\frac{\mathrm{2}{e}^{−{x}} }{\mathrm{1}\:+\:{e}^{−\mathrm{2}{x}} } \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}^{\mathrm{2}} {e}^{−{x}} }{\mathrm{1}+\mathrm{cosh}\:\left({x}\right)}{dx}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−{x}} \underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} {e}^{−\mathrm{2}{kx}} {dx} \\ $$$$=\:\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} \int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−\left(\mathrm{2}{k}+\mathrm{1}\right){x}} {dx}\:=\:\mathrm{4}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$\mathrm{4}\mathfrak{B}\left(\mathrm{3}\right)\:=\:\mathrm{4}\left(\frac{\pi^{\mathrm{3}} }{\mathrm{32}}\right)\:=\:\frac{\pi^{\mathrm{3}} }{\mathrm{8}} \\ $$$${where}\:\mathfrak{B}\left({z}\right)\:{is}\:{the}\:{dirichlet}\:{beta}\:{function} \\ $$$$ \\ $$$$ \\ $$
Commented by MME last updated on 08/Aug/22

$${Boss}\:{mi} \\ $$
Commented by mnjuly1970 last updated on 08/Aug/22
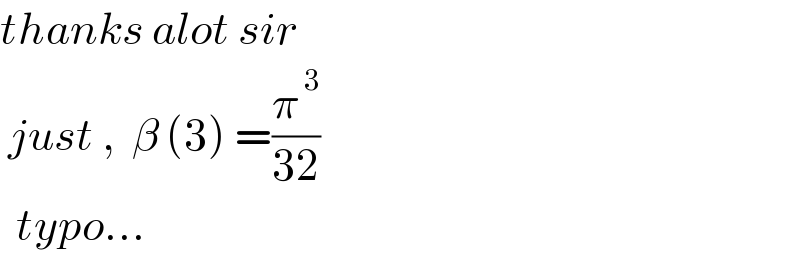
$${thanks}\:{alot}\:{sir} \\ $$$$\:{just}\:,\:\:\beta\:\left(\mathrm{3}\right)\:=\frac{\pi^{\:\mathrm{3}} }{\mathrm{32}} \\ $$$$\:\:{typo}… \\ $$
Commented by princeDera last updated on 08/Aug/22

$${corrected}. \\ $$$${thank}\:{you} \\ $$$$ \\ $$
Commented by princeDera last updated on 08/Aug/22

$$ \\ $$$${my}\:{boss} \\ $$$$ \\ $$
