Question Number 43623 by math khazana by abdo last updated on 12/Sep/18
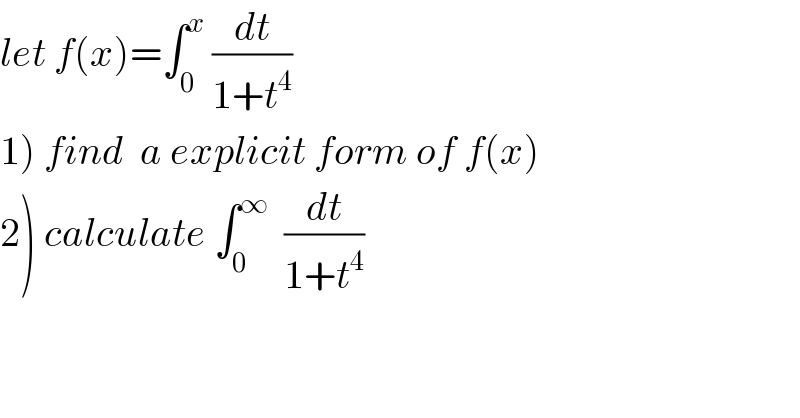
$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\left.\mathrm{1}\right)\:{find}\:\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$
Commented by maxmathsup by imad last updated on 13/Sep/18
![let decompose F(t)=(1/(t^4 +1)) we have F(t)=(1/((t^2 +1)^2 −2t^2 )) =(1/((t^2 +1 −(√2)t)(t^2 +1+(√2)t))) =((at +b)/((t^2 −(√2)t +1))) +((ct +d)/(t^2 +(√2)t +1)) F(−t)=F(t) ⇒((−at +b)/(t^2 +(√2)t +1)) +((−ct +d)/(t^2 −(√2)t +1)) =F(t) ⇒c=−a and b=d ⇒ F(x)=((at +b)/(t^2 −(√2)t +1)) +((−at +b)/(t^2 +(√2)t +1)) F(0) =1 =2b ⇒b=0 ⇒F(t)=((at)/(t^2 −(√2)t +1)) −((at)/(t^2 +(√2)t +1)) F(1) =(1/2) = (a/(2−(√2))) −(a/(2+(√2))) =(((2+(√2)−2+(√2))/2))a =(√2)a ⇒a=(1/(2(√2))) ⇒ F(x)= (1/(2(√2))){ (t/(t^2 −(√2)t +1)) −(t/(t^2 +(√2)t +1))}⇒ ∫ (dt/(1+t^4 )) =(1/(4(√2))){ ∫ ((2t−(√2)+(√2))/(t^2 −(√2)t +1))dt −∫ ((2t +(√2)−(√2))/(t^2 +(√2)t +1))dt} ⇒4(√2) ∫ (dt/(1+t^4 )) =ln∣t^2 −(√2)t +1∣−ln∣t^2 +(√2)t+1∣ +(√2) ∫(dt/(t^2 −(√2)t +1)) −(√2)∫(dt/(t^2 +(√2)t +1)) but ∫ (dt/(t^2 −(√2)t +1)) = ∫ (dt/(t^2 −(2/( (√2)))t +(1/2) +(1/2))) =∫ (dt/((t−(1/( (√2))))^2 +(1/2))) =_(t−(1/( (√2))) =(u/( (√2)))) ∫ (2/(1+u^2 )) (du/( (√2))) =(√2)arctan(u)=(√2)arctan(t(√2)−1) also ∫ (dt/(t^2 +(√2)t +1)) = (√2)arctan(t(√2)+1) ⇒ 4(√2)∫ (dt/(1+t^4 )) =ln∣((t^2 −(√2)t+1)/(t^2 +(√2)t +1))∣ +2 arctan(t(√2)−1)−2 arctan(t(√2)+1) +c ⇒ ∫ (dt/(1+t^4 )) =(1/(4(√2)))ln∣((t^2 −(√2)t +1)/(t^2 +(√2)t +1))∣ +(1/(2(√2))){ arctan(t(√2)−1)−arctan(t(√2)+1)} +c⇒ f(x)= ∫_0 ^x (dt/(1+t^4 )) =[(1/(4(√2)))ln∣((t^2 −(√2)t +1)/(t^2 +(√2)t +1))∣_0 ^x +(1/(2(√2)))[arctan(t(√2)−1)−arctan(t(√2)+1)]_0 ^x f(x)=(1/(4(√2)))ln∣((x^2 −(√2)x +1)/(x^2 +(√2)x +1))∣ +(1/(2(√2))){ arctan(x(√2)−1)−arctan(x(√2)+1) +(π/2)}](https://www.tinkutara.com/question/Q43667.png)
$${let}\:{decompose}\:{F}\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{4}} +\mathrm{1}}\:{we}\:{have}\:{F}\left({t}\right)=\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\:−\sqrt{\mathrm{2}}{t}\right)\left({t}^{\mathrm{2}} +\mathrm{1}+\sqrt{\mathrm{2}}{t}\right)}\:=\frac{{at}\:+{b}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\right)}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$${F}\left(−{t}\right)={F}\left({t}\right)\:\Rightarrow\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\frac{−{ct}\:+{d}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:={F}\left({t}\right)\:\Rightarrow{c}=−{a}\:\:{and}\:{b}={d}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\frac{−{at}\:+{b}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\mathrm{2}{b}\:\Rightarrow{b}=\mathrm{0}\:\:\Rightarrow{F}\left({t}\right)=\frac{{at}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:−\frac{{at}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{{a}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:−\frac{{a}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:=\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}−\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}}\right){a}\:=\sqrt{\mathrm{2}}{a}\:\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:\frac{{t}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:−\frac{{t}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\right\}\Rightarrow \\ $$$$\int\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{\:\:\int\:\:\:\frac{\mathrm{2}{t}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{dt}\:\:−\int\:\:\frac{\mathrm{2}{t}\:+\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{dt}\right\} \\ $$$$\Rightarrow\mathrm{4}\sqrt{\mathrm{2}}\:\int\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:={ln}\mid{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\mid−{ln}\mid{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}+\mathrm{1}\mid\:+\sqrt{\mathrm{2}}\:\:\int\frac{{dt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:−\sqrt{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$${but}\:\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:=\:\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}}{t}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}}\:=\int\:\frac{{dt}}{\left({t}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=_{{t}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:=\frac{{u}}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\:\int\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{1}+{u}^{\mathrm{2}} }\:\frac{{du}}{\:\sqrt{\mathrm{2}}}\:=\sqrt{\mathrm{2}}{arctan}\left({u}\right)=\sqrt{\mathrm{2}}{arctan}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)\:{also} \\ $$$$\int\:\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:=\:\sqrt{\mathrm{2}}{arctan}\left({t}\sqrt{\mathrm{2}}+\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{4}\sqrt{\mathrm{2}}\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:={ln}\mid\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\mid\:+\mathrm{2}\:{arctan}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)−\mathrm{2}\:{arctan}\left({t}\sqrt{\mathrm{2}}+\mathrm{1}\right)\:+{c}\:\Rightarrow \\ $$$$\int\:\:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:{arctan}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)−{arctan}\left({t}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right\}\:+{c}\Rightarrow \\ $$$${f}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\left[\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\mid_{\mathrm{0}} ^{{x}} \:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left[{arctan}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)−{arctan}\left({t}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{{x}} \right. \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:{arctan}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)−{arctan}\left({x}\sqrt{\mathrm{2}}+\mathrm{1}\right)\:+\frac{\pi}{\mathrm{2}}\right\} \\ $$$$ \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 13/Sep/18
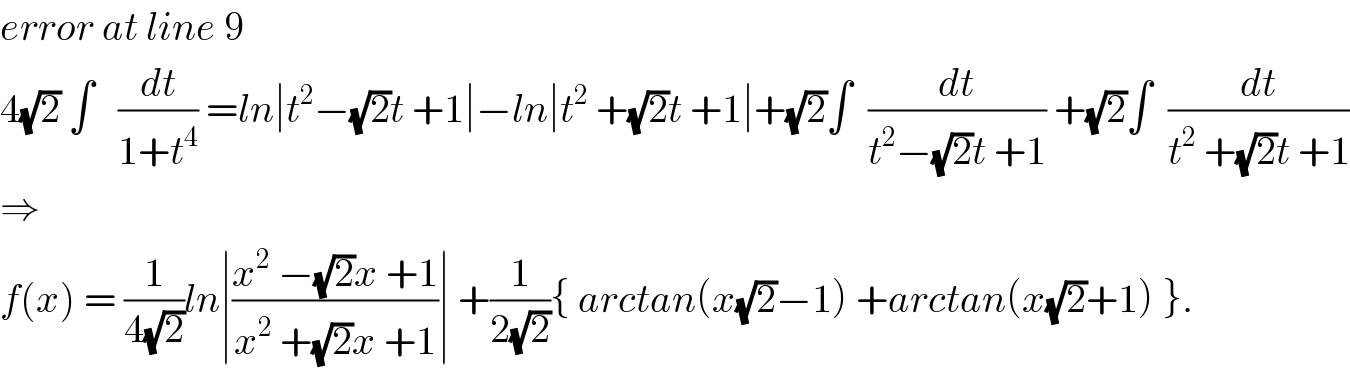
$${error}\:{at}\:{line}\:\mathrm{9} \\ $$$$\mathrm{4}\sqrt{\mathrm{2}}\:\int\:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:={ln}\mid{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\mid−{ln}\mid{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}\mid+\sqrt{\mathrm{2}}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\:+\sqrt{\mathrm{2}}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{t}\:+\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{x}^{\mathrm{2}} \:−\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+\sqrt{\mathrm{2}}{x}\:+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:{arctan}\left({x}\sqrt{\mathrm{2}}−\mathrm{1}\right)\:+{arctan}\left({x}\sqrt{\mathrm{2}}+\mathrm{1}\right)\:\right\}. \\ $$
Commented by maxmathsup by imad last updated on 13/Sep/18
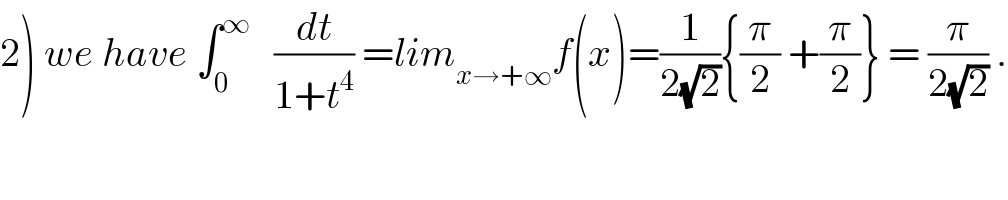
$$\left.\mathrm{2}\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:={lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\frac{\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\right\}\:=\:\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\:. \\ $$$$\: \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Sep/18
![∫(dt/(1+t^4 )) ∫((1/t^2 )/(t^2 +(1/t^2 )))dt (1/2)∫(((1+(1/t^2 ))−(1−(1/t^2 )))/(t^2 +(1/t^2 )))dt (1/2)∫((d(t−(1/t)))/((t−(1/t))^2 +2))−(1/2)∫((d(t+(1/t)))/((t+(1/t))^2 −2)) I_1 =(1/2)∫((d(t−(1/t)))/((t−(1/t))^2 +2)) =(1/2)×(1/( (√2) ))tan^(−1) (((t−(1/t))/( (√2))))+c I_2 =(1/2)∫((d(t+(1/t)))/((t+(1/t))^2 −((√2) )^2 )) formula∫(dy/(y^2 −a^2 ))=(1/(2a))∫(((y+a)−(y−a))/((y+a)y−a)))dy (1/(2a))[∫(dy/(y−a))−∫(dy/(y+a))] (1/(2a))ln∣((y−a)/(y+a))∣+c_2 I_2 =(1/2)×(1/(2(√2)))ln∣((t+(1/t)−(√2))/(t+(1/t)+(√2)))∣ so ans is I_1 −I_2 (1/(2(√2)))tan^(−1) (((t−(1/t))/( (√2))))−(1/(4(√2)))ln∣((t+(1/t)−(√2))/(t+(1/t)+(√2)))∣+c so ∫_0 ^x (dt/(1+t^4 )) [(1/(2(√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/(4(√2)))ln∣((x+(1/x)−(√2))/(x+(1/x)+(√2)))∣]− [(1/(2(√2)))tan^(−1) (−∞)−0 (1/(2(√2)))(−(Π/2)) ans is[ (1/(2(√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/(4(√2)))ln∣((x+(1/x)−(√2))/(x+(1/x)+(√2)))∣+(Π/(4(√2)))](https://www.tinkutara.com/question/Q43651.png)
$$\int\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\int\frac{\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}+\frac{\mathrm{1}}{{t}}\right)}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\mathrm{1}}{{t}}}{\:\sqrt{\mathrm{2}}}\right)+{c} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({t}+\frac{\mathrm{1}}{{t}}\right)}{\left({t}+\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} } \\ $$$${formula}\int\frac{{dy}}{{y}^{\mathrm{2}} −{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}\int\frac{\left({y}+{a}\right)−\left({y}−{a}\right)}{\left.\left({y}+{a}\right){y}−{a}\right)}{dy} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}}\left[\int\frac{{dy}}{{y}−{a}}−\int\frac{{dy}}{{y}+{a}}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\mid\frac{{y}−{a}}{{y}+{a}}\mid+{c}_{\mathrm{2}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{2}}}{{t}+\frac{\mathrm{1}}{{t}}+\sqrt{\mathrm{2}}}\mid \\ $$$${so}\:{ans}\:{is}\:{I}_{\mathrm{1}} −{I}_{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{t}−\frac{\mathrm{1}}{{t}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}+\frac{\mathrm{1}}{{t}}−\sqrt{\mathrm{2}}}{{t}+\frac{\mathrm{1}}{{t}}+\sqrt{\mathrm{2}}}\mid+{c} \\ $$$${so} \\ $$$$\int_{\mathrm{0}} ^{{x}} \frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\mid\right]− \\ $$$$\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(−\infty\right)−\mathrm{0}\right. \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left(−\frac{\Pi}{\mathrm{2}}\right) \\ $$$${ans}\:{is}\left[\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\mid+\frac{\Pi}{\mathrm{4}\sqrt{\mathrm{2}}}\right. \\ $$$$ \\ $$$$ \\ $$
