Question Number 43659 by Joel578 last updated on 13/Sep/18
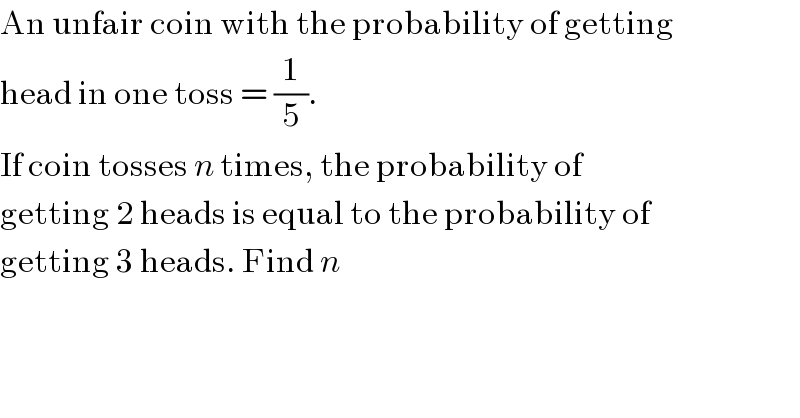
$$\mathrm{An}\:\mathrm{unfair}\:\mathrm{coin}\:\mathrm{with}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\:\mathrm{getting} \\ $$$$\mathrm{head}\:\mathrm{in}\:\mathrm{one}\:\mathrm{toss}\:=\:\frac{\mathrm{1}}{\mathrm{5}}. \\ $$$$\mathrm{If}\:\mathrm{coin}\:\mathrm{tosses}\:{n}\:\mathrm{times},\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of} \\ $$$$\mathrm{getting}\:\mathrm{2}\:\mathrm{heads}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{of}\: \\ $$$$\mathrm{getting}\:\mathrm{3}\:\mathrm{heads}.\:\mathrm{Find}\:{n} \\ $$
Commented by math1967 last updated on 14/Sep/18

$${n}=\mathrm{14}? \\ $$
Commented by Joel578 last updated on 17/Sep/18

$$\mathrm{Please}\:\mathrm{explain}\:\mathrm{the}\:\mathrm{working}\:\mathrm{Sir} \\ $$
Answered by math1967 last updated on 17/Sep/18
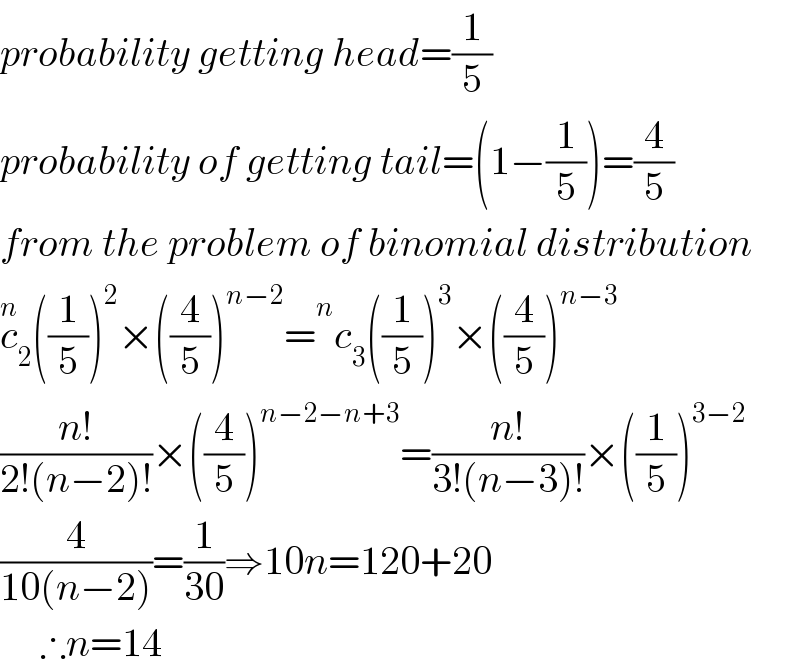
$${probability}\:{getting}\:{head}=\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${probability}\:{of}\:{getting}\:{tail}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}\right)=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${from}\:{the}\:{problem}\:{of}\:{binomial}\:{distribution} \\ $$$$\overset{{n}} {{c}}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{2}} ×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{n}−\mathrm{2}} =\overset{{n}} {\:}{c}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{3}} ×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{n}−\mathrm{3}} \\ $$$$\frac{{n}!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{{n}−\mathrm{2}−{n}+\mathrm{3}} =\frac{{n}!}{\mathrm{3}!\left({n}−\mathrm{3}\right)!}×\left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{3}−\mathrm{2}} \\ $$$$\frac{\mathrm{4}}{\mathrm{10}\left({n}−\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{30}}\Rightarrow\mathrm{10}{n}=\mathrm{120}+\mathrm{20} \\ $$$$\:\:\:\:\:\therefore{n}=\mathrm{14} \\ $$
