Question Number 43679 by gunawan last updated on 14/Sep/18

$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{i}^{\mathrm{2}} }{\mathrm{2}^{{i}} \:}=… \\ $$
Commented by abdo.msup.com last updated on 14/Sep/18
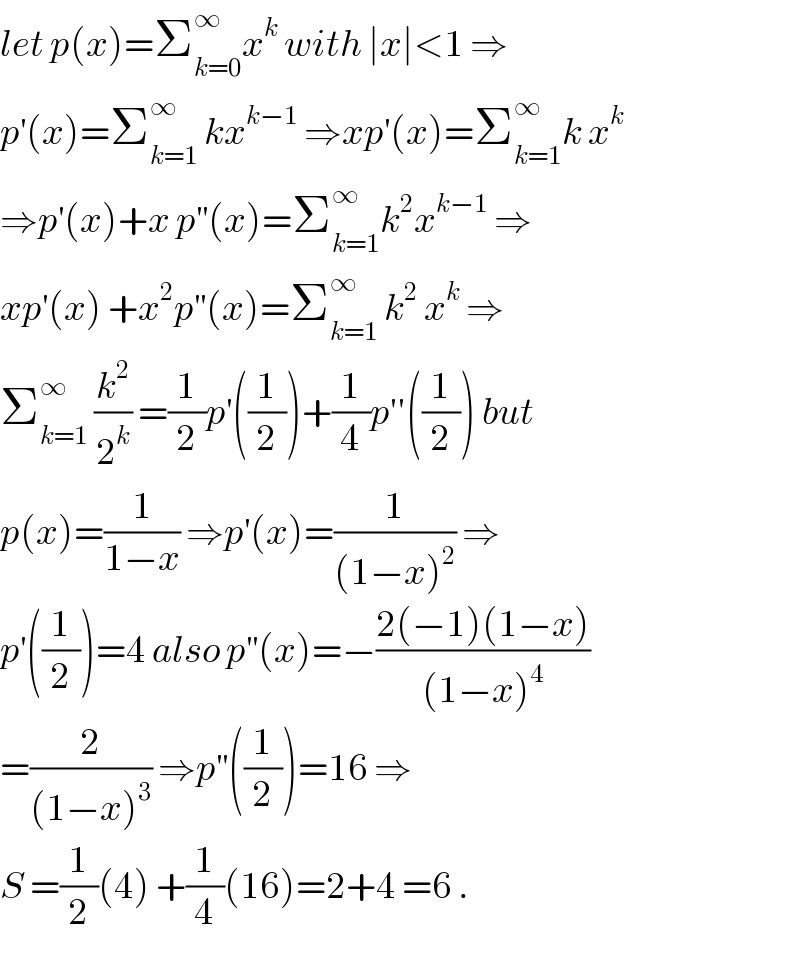
$${let}\:{p}\left({x}\right)=\sum_{{k}=\mathrm{0}} ^{\infty} {x}^{{k}} \:{with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$${p}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} \:{kx}^{{k}−\mathrm{1}} \:\Rightarrow{xp}^{'} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} {k}\:{x}^{{k}} \\ $$$$\Rightarrow{p}^{'} \left({x}\right)+{x}\:{p}^{''} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} {k}^{\mathrm{2}} {x}^{{k}−\mathrm{1}} \:\Rightarrow \\ $$$${xp}^{'} \left({x}\right)\:+{x}^{\mathrm{2}} {p}^{''} \left({x}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} \:{k}^{\mathrm{2}} \:{x}^{{k}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{{k}^{\mathrm{2}} }{\mathrm{2}^{{k}} }\:=\frac{\mathrm{1}}{\mathrm{2}}{p}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}}{p}''\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:{but} \\ $$$${p}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow{p}^{'} \left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$${p}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{4}\:{also}\:{p}^{''} \left({x}\right)=−\frac{\mathrm{2}\left(−\mathrm{1}\right)\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }\:\Rightarrow{p}^{''} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{16}\:\Rightarrow \\ $$$${S}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{16}\right)=\mathrm{2}+\mathrm{4}\:=\mathrm{6}\:. \\ $$
