Question Number 43683 by Raj Singh last updated on 14/Sep/18
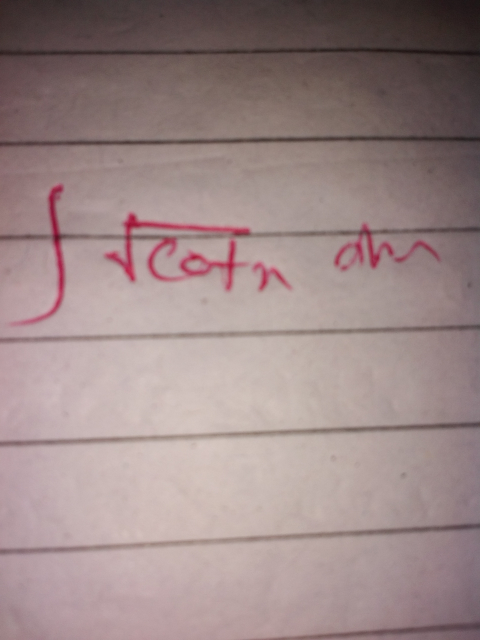
Commented by Meritguide1234 last updated on 14/Sep/18
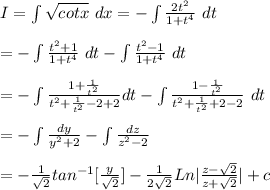
Commented by maxmathsup by imad last updated on 15/Sep/18

$${let}\:{I}\:=\:\int\:\sqrt{{cotanx}}{dx}\:\Rightarrow\:{I}\:=\:\int\:\frac{{dx}}{\:\sqrt{{tanx}}}\:{changement}\:\sqrt{{tanx}}={t}\:{give} \\ $$$${tanx}\:={t}^{\mathrm{2}} \:\Rightarrow{x}\:={arctan}\left({t}^{\mathrm{2}} \right)\:\Rightarrow\:{dx}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}\:\Rightarrow\:{I}\:=\:\int\:\frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{4}} \right){t}}{dt} \\ $$$$=\mathrm{2}\:\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:\:{but}\:{we}\:{have}\:{proved}\:{that}\: \\ $$$$\int\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}{ln}\mid\frac{{t}^{\mathrm{2}} \:−\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}{{t}^{\mathrm{2}} +\sqrt{\mathrm{2}}{t}\:+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\left\{\:{arctan}\left({t}\sqrt{\mathrm{2}}−\mathrm{1}\right)\:+{arctan}\left({t}\sqrt{\mathrm{2}}+\mathrm{1}\right)\right\}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\mid\:\frac{{tanx}\:−\sqrt{\mathrm{2}{tanx}}+\mathrm{1}}{{tanx}\:+\sqrt{\mathrm{2}{tanx}}\:+\mathrm{1}}\mid\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\:{arctan}\left(\sqrt{\mathrm{2}{tanx}}−\mathrm{1}\right)+{arctan}\left(\sqrt{\mathrm{2}{tanx}}\:+\mathrm{1}\right)\right\} \\ $$
