Question-174776

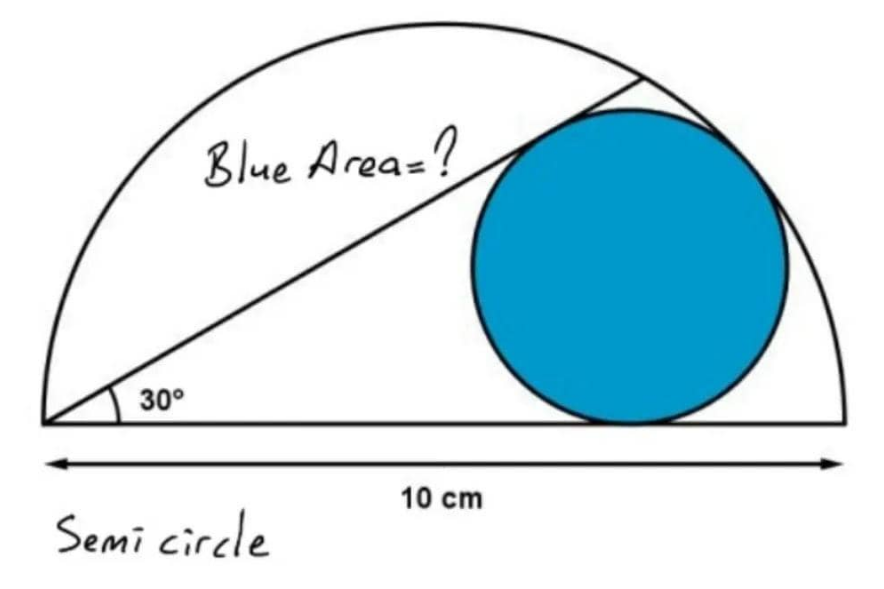
Question Number 174776 by Tawa11 last updated on 10/Aug/22

Answered by aleks041103 last updated on 11/Aug/22

Commented by aleks041103 last updated on 11/Aug/22

R=5 r=? OA=R−r=5−r AB=r ⇒OB=(√((5−r)^2 −r^2 ))=(√(5(5−2r))) tg(ACB)=(r/(5+(√(5(5−2r))))) CA is the angle bisector of C, since A is the center of a circle whose tangents intersect at C. ⇒ACB=15° now if we know tg(15°)=t^(−1) we can find r. 5+(√(5(5−2r)))=rt ⇒(rt−5)^2 =25−10r t^2 r^2 −10tr+10r=0 ⇒t^2 r−10(t−1)=0 ⇒r=((10(t−1))/t^2 ) tg(30)=((2tg(15))/(1−tg^2 (15)))=(2/(t(1−(1/t^2 ))))=((2t)/(t^2 −1))=(1/( (√3))) t^2 −2(√3)t−1=0 t_(1,2) =((2(√3)±(√(12+4)))/2)=(√3)±2 t>0 ⇒t=2+(√3) ⇒r=((10(1+(√3)))/(7+4(√3)))

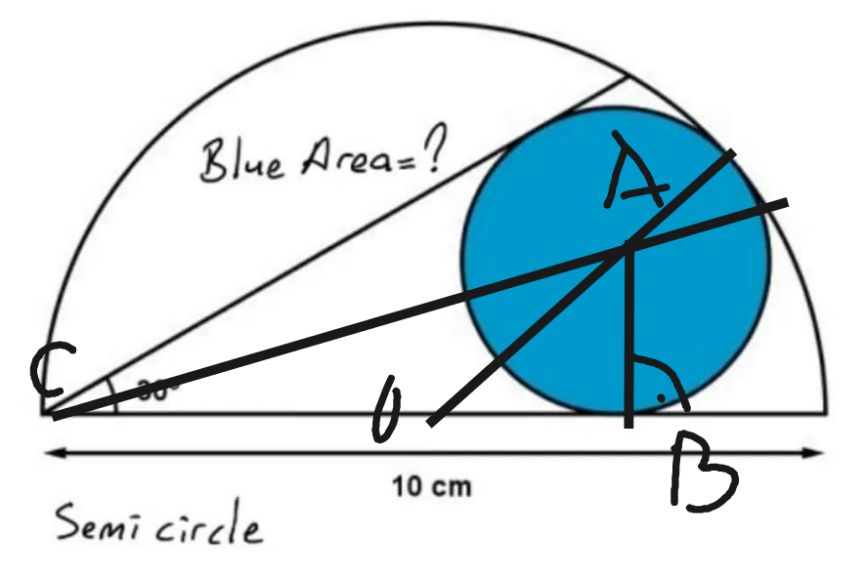
$${R}=\mathrm{5} \\ $$$${r}=? \\ $$$${OA}={R}−{r}=\mathrm{5}−{r} \\ $$$${AB}={r} \\ $$$$\Rightarrow{OB}=\sqrt{\left(\mathrm{5}−{r}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}{r}\right)} \\ $$$${tg}\left({ACB}\right)=\frac{{r}}{\mathrm{5}+\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}{r}\right)}} \\ $$$${CA}\:{is}\:{the}\:{angle}\:{bisector}\:{of}\:{C},\:{since}\: \\ $$$${A}\:{is}\:{the}\:{center}\:{of}\:{a}\:{circle}\:{whose}\:{tangents}\: \\ $$$${intersect}\:{at}\:{C}. \\ $$$$\Rightarrow{ACB}=\mathrm{15}° \\ $$$${now}\:{if}\:{we}\:{know}\:{tg}\left(\mathrm{15}°\right)={t}^{−\mathrm{1}} \:{we}\:{can}\:{find}\:{r}. \\ $$$$\mathrm{5}+\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}{r}\right)}={rt} \\ $$$$\Rightarrow\left({rt}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{25}−\mathrm{10}{r} \\ $$$${t}^{\mathrm{2}} {r}^{\mathrm{2}} −\mathrm{10}{tr}+\mathrm{10}{r}=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{2}} {r}−\mathrm{10}\left({t}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{r}=\frac{\mathrm{10}\left({t}−\mathrm{1}\right)}{{t}^{\mathrm{2}} } \\ $$$${tg}\left(\mathrm{30}\right)=\frac{\mathrm{2}{tg}\left(\mathrm{15}\right)}{\mathrm{1}−{tg}^{\mathrm{2}} \left(\mathrm{15}\right)}=\frac{\mathrm{2}}{{t}\left(\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{3}}{t}−\mathrm{1}=\mathrm{0} \\ $$$${t}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{2}\sqrt{\mathrm{3}}\pm\sqrt{\mathrm{12}+\mathrm{4}}}{\mathrm{2}}=\sqrt{\mathrm{3}}\pm\mathrm{2} \\ $$$${t}>\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{10}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)}{\mathrm{7}+\mathrm{4}\sqrt{\mathrm{3}}} \\ $$

Commented by Tawa11 last updated on 11/Aug/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by peter frank last updated on 11/Aug/22

$$\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply