f-x-f-2x-y-5xy-f-3x-y-x-2-1-for-every-x-y-R-find-f-10-

Question Number 109262 by bemath last updated on 22/Aug/20

$${f}\left({x}\right)+{f}\left(\mathrm{2}{x}+{y}\right)+\mathrm{5}{xy}\:=\:{f}\left(\mathrm{3}{x}−{y}\right)+{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${for}\:{every}\:{x},{y}\in\mathbb{R}\:.\:{find}\:{f}\left(\mathrm{10}\right) \\ $$

Answered by mr W last updated on 22/Aug/20

y=0: f(x)+f(2x) = f(3x)+x^2 +1 ...(i) y=x: f(x)+f(3x)+5x^2 = f(2x)+x^2 +1 ...(ii) (i)+(ii): 2f(x)+f(2x)+f(3x)+5x^2 =f(3x)+x^2 +1+f(2x)+x^2 +1 2f(x)=−3x^2 +2 ⇒f(x)=−(3/2)x^2 +1 ⇒f(10)=−(3/2)×10^2 +1=−149

$${y}=\mathrm{0}: \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{2}{x}\right)\:=\:{f}\left(\mathrm{3}{x}\right)+{x}^{\mathrm{2}} +\mathrm{1}\:\:\:…\left({i}\right) \\ $$$${y}={x}: \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{3}{x}\right)+\mathrm{5}{x}^{\mathrm{2}} \:=\:{f}\left(\mathrm{2}{x}\right)+{x}^{\mathrm{2}} +\mathrm{1}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{2}{f}\left({x}\right)+{f}\left(\mathrm{2}{x}\right)+{f}\left(\mathrm{3}{x}\right)+\mathrm{5}{x}^{\mathrm{2}} ={f}\left(\mathrm{3}{x}\right)+{x}^{\mathrm{2}} +\mathrm{1}+{f}\left(\mathrm{2}{x}\right)+{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{2}{f}\left({x}\right)=−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2} \\ $$$$\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow{f}\left(\mathrm{10}\right)=−\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{10}^{\mathrm{2}} +\mathrm{1}=−\mathrm{149} \\ $$

Answered by Rasheed.Sindhi last updated on 22/Aug/20

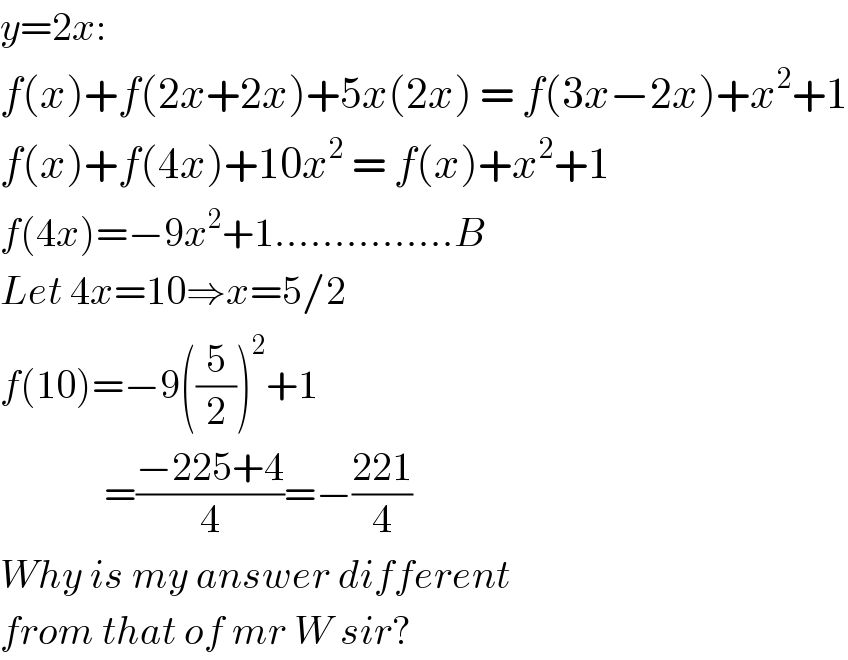
y=2x: f(x)+f(2x+2x)+5x(2x) = f(3x−2x)+x^2 +1 f(x)+f(4x)+10x^2 = f(x)+x^2 +1 f(4x)=−9x^2 +1...............B Let 4x=10⇒x=5/2 f(10)=−9((5/2))^2 +1 =((−225+4)/4)=−((221)/4) Why is my answer different from that of mr W sir?

$${y}=\mathrm{2}{x}: \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{2}{x}+\mathrm{2}{x}\right)+\mathrm{5}{x}\left(\mathrm{2}{x}\right)\:=\:{f}\left(\mathrm{3}{x}−\mathrm{2}{x}\right)+{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{4}{x}\right)+\mathrm{10}{x}^{\mathrm{2}} \:=\:{f}\left({x}\right)+{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${f}\left(\mathrm{4}{x}\right)=−\mathrm{9}{x}^{\mathrm{2}} +\mathrm{1}……………{B} \\ $$$${Let}\:\mathrm{4}{x}=\mathrm{10}\Rightarrow{x}=\mathrm{5}/\mathrm{2} \\ $$$${f}\left(\mathrm{10}\right)=−\mathrm{9}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−\mathrm{225}+\mathrm{4}}{\mathrm{4}}=−\frac{\mathrm{221}}{\mathrm{4}} \\ $$$${Why}\:{is}\:{my}\:{answer}\:{different}\: \\ $$$${from}\:{that}\:{of}\:{mr}\:{W}\:{sir}? \\ $$

Commented by mr W last updated on 22/Aug/20

it means that f(x)+f(2x+y)+5xy = f(3x−y)+x^2 +1 is not consistent because it leads to contradiction.

$${it}\:{means}\:{that} \\ $$$${f}\left({x}\right)+{f}\left(\mathrm{2}{x}+{y}\right)+\mathrm{5}{xy}\:=\:{f}\left(\mathrm{3}{x}−{y}\right)+{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${is}\:{not}\:{consistent}\:{because}\:{it}\:{leads}\:{to} \\ $$$${contradiction}. \\ $$

Commented by Rasheed.Sindhi last updated on 22/Aug/20