Menu Close

Question-109342

Tinku Tara 0 Comments
Pin




Question Number 109342 by 150505R last updated on 22/Aug/20
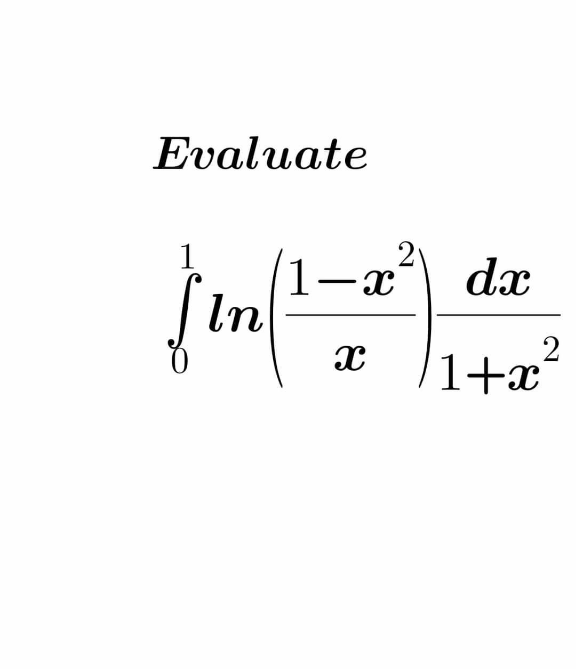
Commented by maths mind last updated on 23/Aug/20
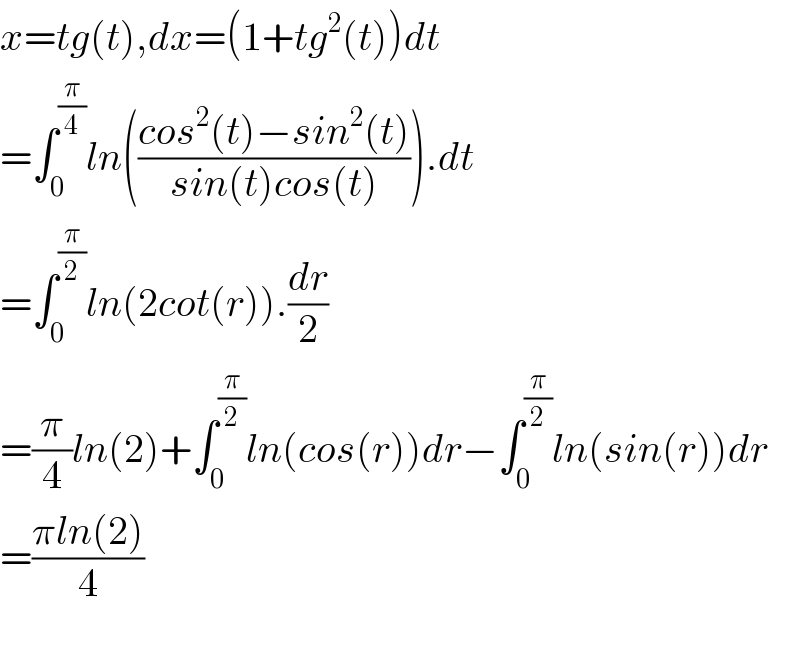
x=tg(t),dx=(1+tg^2 (t))dt =∫_0 ^(π/4) ln(((cos^2 (t)−sin^2 (t))/(sin(t)cos(t)))).dt =∫_0 ^(π/2) ln(2cot(r)).(dr/2) =(π/4)ln(2)+∫_0 ^(π/2) ln(cos(r))dr−∫_0 ^(π/2) ln(sin(r))dr =((πln(2))/4)
$${x}={tg}\left({t}\right),{dx}=\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\frac{{cos}^{\mathrm{2}} \left({t}\right)−{sin}^{\mathrm{2}} \left({t}\right)}{{sin}\left({t}\right){cos}\left({t}\right)}\right).{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{2}{cot}\left({r}\right)\right).\frac{{dr}}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{4}}{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({r}\right)\right){dr}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({r}\right)\right){dr} \\ $$$$=\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$ \\ $$
Commented by mathdave last updated on 23/Aug/20
you should ve explain better how you change ((cos^2 t−sin^2 t)/(sintcost))=2cot(r) for those that are not pro like u . let me put light on that area
$${you}\:{should}\:{ve}\:{explain}\:{better}\:{how}\:{you}\:{change}\: \\ $$$$\frac{\mathrm{cos}^{\mathrm{2}} {t}−\mathrm{sin}^{\mathrm{2}} {t}}{\mathrm{sin}{t}\mathrm{cos}{t}}=\mathrm{2cot}\left({r}\right)\:{for}\:{those}\:{that}\:{are}\:{not}\:{pro} \\ $$$${like}\:{u}\:. \\ $$$${let}\:{me}\:{put}\:{light}\:{on}\:{that}\:{area}\: \\ $$$$ \\ $$
Commented by mathdave last updated on 23/Aug/20
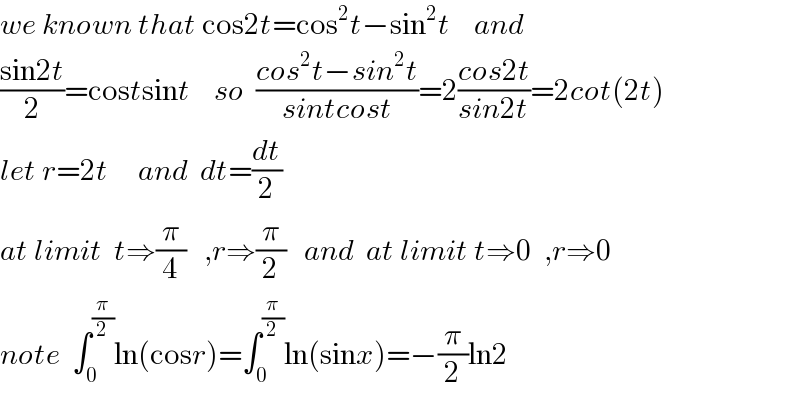
we known that cos2t=cos^2 t−sin^2 t and ((sin2t)/2)=costsint so ((cos^2 t−sin^2 t)/(sintcost))=2((cos2t)/(sin2t))=2cot(2t) let r=2t and dt=(dt/2) at limit t⇒(π/4) ,r⇒(π/2) and at limit t⇒0 ,r⇒0 note ∫_0 ^(π/2) ln(cosr)=∫_0 ^(π/2) ln(sinx)=−(π/2)ln2
$${we}\:{known}\:{that}\:\mathrm{cos2}{t}=\mathrm{cos}^{\mathrm{2}} {t}−\mathrm{sin}^{\mathrm{2}} {t}\:\:\:\:{and} \\ $$$$\frac{\mathrm{sin2}{t}}{\mathrm{2}}=\mathrm{cos}{t}\mathrm{sin}{t}\:\:\:\:{so}\:\:\frac{{cos}^{\mathrm{2}} {t}−{sin}^{\mathrm{2}} {t}}{{sintcost}}=\mathrm{2}\frac{{cos}\mathrm{2}{t}}{{sin}\mathrm{2}{t}}=\mathrm{2}{cot}\left(\mathrm{2}{t}\right) \\ $$$${let}\:{r}=\mathrm{2}{t}\:\:\:\:\:{and}\:\:{dt}=\frac{{dt}}{\mathrm{2}} \\ $$$${at}\:{limit}\:\:{t}\Rightarrow\frac{\pi}{\mathrm{4}}\:\:\:,{r}\Rightarrow\frac{\pi}{\mathrm{2}}\:\:\:{and}\:\:{at}\:{limit}\:{t}\Rightarrow\mathrm{0}\:\:,{r}\Rightarrow\mathrm{0} \\ $$$${note}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{r}\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right)=−\frac{\pi}{\mathrm{2}}\mathrm{ln2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *