Question Number 135437 by 0731619177 last updated on 13/Mar/21
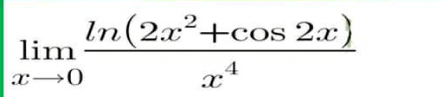
Answered by EDWIN88 last updated on 13/Mar/21
![L′Ho^� pital lim_(x→0) (((4x−2sin 2x)/(2x^2 +cos 2x))/(4x^3 )) = lim_(x→0) (1/(2x^2 +cos 2x)).lim_(x→0) ((4x−2sin 2x )/(4x^3 )) = (1/1). lim_(x→0) ((4−4cos 2x)/(12x^2 )) = (1/3).lim_(x→0) ((1−(1−2sin^2 x))/x^2 ) =(2/3).[ lim_(x→0) ((sin x)/x) ]^2 = (2/3)](https://www.tinkutara.com/question/Q135462.png)
$$\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{4x}−\mathrm{2sin}\:\mathrm{2x}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{cos}\:\mathrm{2x}}}{\mathrm{4x}^{\mathrm{3}} }\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2x}^{\mathrm{2}} +\mathrm{cos}\:\mathrm{2x}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4x}−\mathrm{2sin}\:\mathrm{2x}\:}{\mathrm{4x}^{\mathrm{3}} } \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{1}}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4}−\mathrm{4cos}\:\mathrm{2x}}{\mathrm{12x}^{\mathrm{2}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}.\left[\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\:\right]^{\mathrm{2}} \:=\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by mathmax by abdo last updated on 13/Mar/21
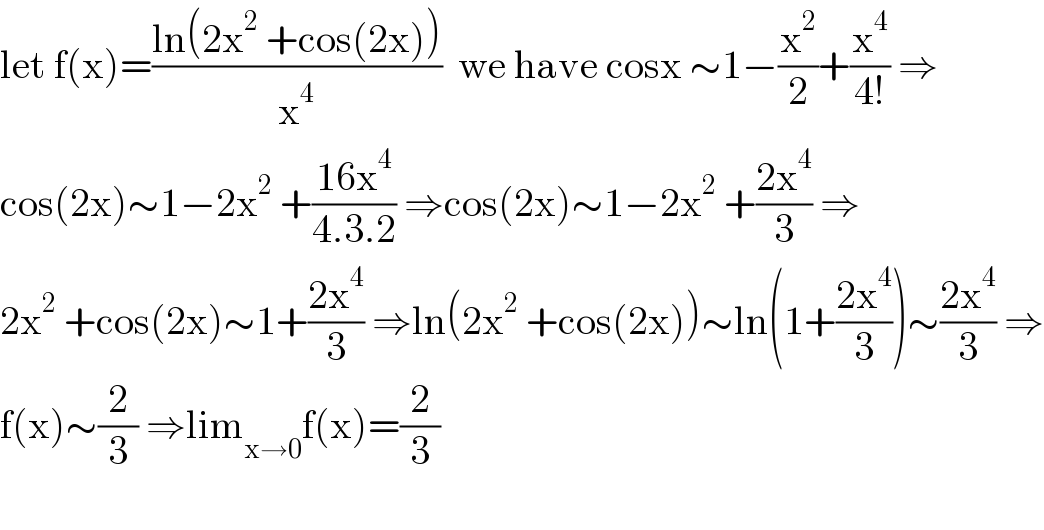
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{ln}\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{cos}\left(\mathrm{2x}\right)\right)}{\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{cosx}\:\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{4}!}\:\Rightarrow \\ $$$$\mathrm{cos}\left(\mathrm{2x}\right)\sim\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \:+\frac{\mathrm{16x}^{\mathrm{4}} }{\mathrm{4}.\mathrm{3}.\mathrm{2}}\:\Rightarrow\mathrm{cos}\left(\mathrm{2x}\right)\sim\mathrm{1}−\mathrm{2x}^{\mathrm{2}} \:+\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{2x}^{\mathrm{2}} \:+\mathrm{cos}\left(\mathrm{2x}\right)\sim\mathrm{1}+\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{3}}\:\Rightarrow\mathrm{ln}\left(\mathrm{2x}^{\mathrm{2}} \:+\mathrm{cos}\left(\mathrm{2x}\right)\right)\sim\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{3}}\right)\sim\frac{\mathrm{2x}^{\mathrm{4}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Commented by 0731619177 last updated on 13/Mar/21

$${thanks} \\ $$
