Question Number 109401 by john santu last updated on 23/Aug/20
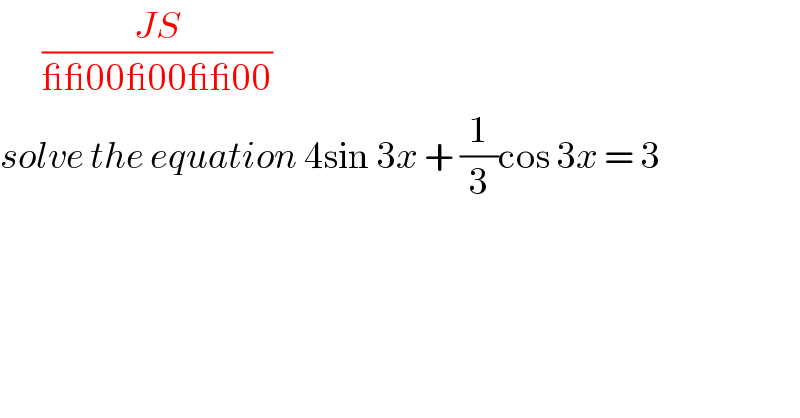
$$\:\:\:\:\:\:\:\frac{{JS}}{\_\_\mathrm{00\_00\_\_00}} \\ $$$${solve}\:{the}\:{equation}\:\mathrm{4sin}\:\mathrm{3}{x}\:+\:\frac{\mathrm{1}}{\mathrm{3}}\mathrm{cos}\:\mathrm{3}{x}\:=\:\mathrm{3} \\ $$
Answered by mr W last updated on 23/Aug/20

$$\mathrm{12}\:\mathrm{sin}\:\mathrm{3}{x}+\mathrm{cos}\:\mathrm{3}{x}=\mathrm{9} \\ $$$$\frac{\mathrm{12}}{\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\:\mathrm{sin}\:\mathrm{3}{x}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}\mathrm{cos}\:\mathrm{3}{x}=\frac{\mathrm{9}}{\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }} \\ $$$$\mathrm{sin}\:\alpha\:\mathrm{sin}\:\mathrm{3}{x}+\mathrm{cos}\:\alpha\:\mathrm{cos}\:\mathrm{3}{x}=\frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}} \\ $$$$\mathrm{cos}\:\left(\mathrm{3}{x}−\alpha\right)=\frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}} \\ $$$$\mathrm{3}{x}−\alpha=\mathrm{2}{k}\pi\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{k}\pi+\alpha\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}{k}\pi+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{145}}}\pm\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}}\right) \\ $$
Answered by ajfour last updated on 24/Aug/20
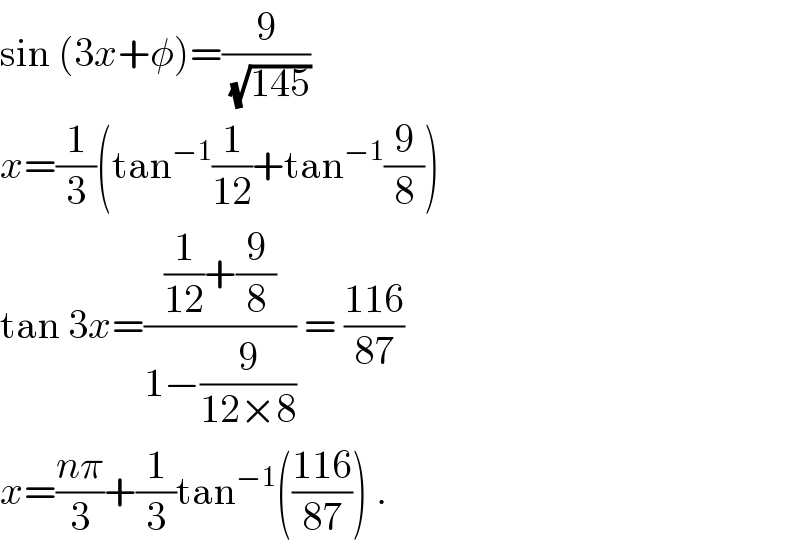
$$\mathrm{sin}\:\left(\mathrm{3}{x}+\phi\right)=\frac{\mathrm{9}}{\:\sqrt{\mathrm{145}}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{12}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{9}}{\mathrm{8}}\right) \\ $$$$\mathrm{tan}\:\mathrm{3}{x}=\frac{\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{9}}{\mathrm{8}}}{\mathrm{1}−\frac{\mathrm{9}}{\mathrm{12}×\mathrm{8}}}\:=\:\frac{\mathrm{116}}{\mathrm{87}} \\ $$$${x}=\frac{{n}\pi}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{116}}{\mathrm{87}}\right)\:. \\ $$
Commented by mr W last updated on 23/Aug/20

$${nice}\:{solution}! \\ $$
Answered by 1549442205PVT last updated on 23/Aug/20
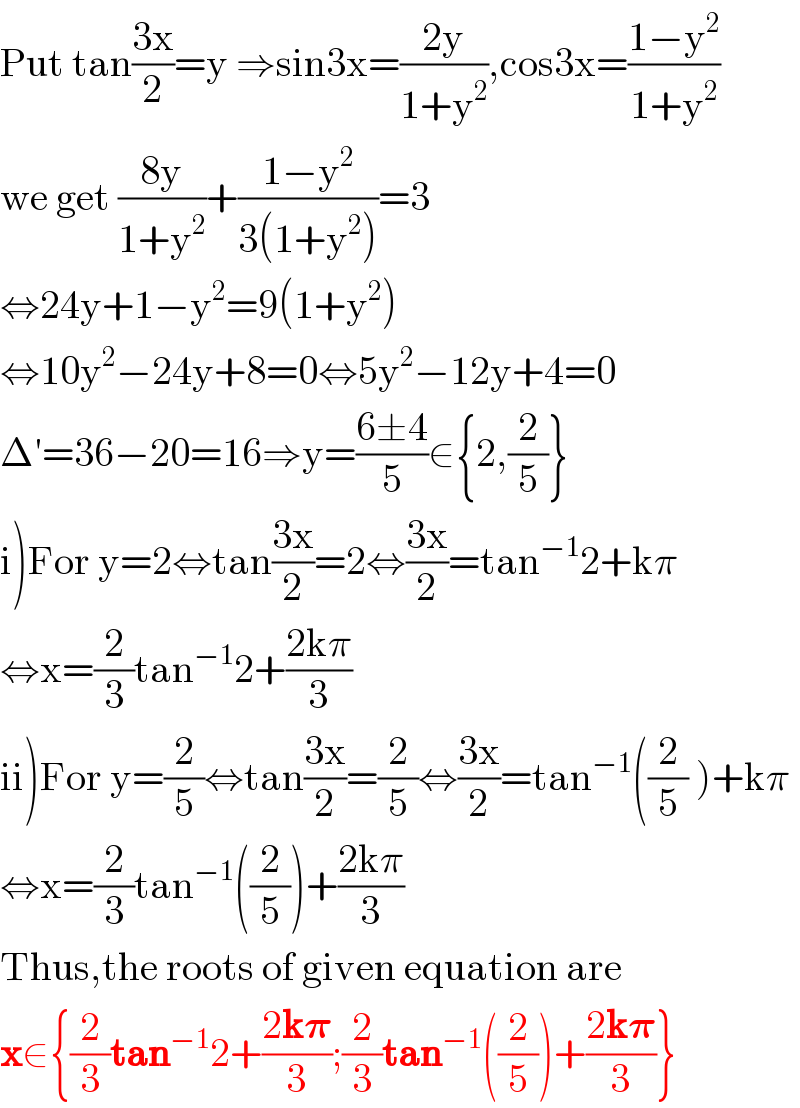
$$\mathrm{Put}\:\mathrm{tan}\frac{\mathrm{3x}}{\mathrm{2}}=\mathrm{y}\:\Rightarrow\mathrm{sin3x}=\frac{\mathrm{2y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} },\mathrm{cos3x}=\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{get}\:\frac{\mathrm{8y}}{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{3}\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)}=\mathrm{3} \\ $$$$\Leftrightarrow\mathrm{24y}+\mathrm{1}−\mathrm{y}^{\mathrm{2}} =\mathrm{9}\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right) \\ $$$$\Leftrightarrow\mathrm{10y}^{\mathrm{2}} −\mathrm{24y}+\mathrm{8}=\mathrm{0}\Leftrightarrow\mathrm{5y}^{\mathrm{2}} −\mathrm{12y}+\mathrm{4}=\mathrm{0} \\ $$$$\Delta'=\mathrm{36}−\mathrm{20}=\mathrm{16}\Rightarrow\mathrm{y}=\frac{\mathrm{6}\pm\mathrm{4}}{\mathrm{5}}\in\left\{\mathrm{2},\frac{\mathrm{2}}{\mathrm{5}}\right\} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{y}=\mathrm{2}\Leftrightarrow\mathrm{tan}\frac{\mathrm{3x}}{\mathrm{2}}=\mathrm{2}\Leftrightarrow\frac{\mathrm{3x}}{\mathrm{2}}=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{k}\pi \\ $$$$\Leftrightarrow\mathrm{x}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \mathrm{2}+\frac{\mathrm{2k}\pi}{\mathrm{3}} \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{y}=\frac{\mathrm{2}}{\mathrm{5}}\Leftrightarrow\mathrm{tan}\frac{\mathrm{3x}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{5}}\Leftrightarrow\frac{\mathrm{3x}}{\mathrm{2}}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\:\right)+\mathrm{k}\pi \\ $$$$\Leftrightarrow\mathrm{x}=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)+\frac{\mathrm{2k}\pi}{\mathrm{3}} \\ $$$$\mathrm{Thus},\mathrm{the}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{are} \\ $$$$\boldsymbol{\mathrm{x}}\in\left\{\frac{\mathrm{2}}{\mathrm{3}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \mathrm{2}+\frac{\mathrm{2}\boldsymbol{\mathrm{k}\pi}}{\mathrm{3}};\frac{\mathrm{2}}{\mathrm{3}}\boldsymbol{\mathrm{tan}}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{\mathrm{5}}\right)+\frac{\mathrm{2}\boldsymbol{\mathrm{k}\pi}}{\mathrm{3}}\right\} \\ $$
