Menu Close

dx-x-2-a-2-ln-x-x-2-a-2-C-Proof-

Tinku Tara 0 Comments
Pin




Question Number 109403 by abony1303 last updated on 23/Aug/20
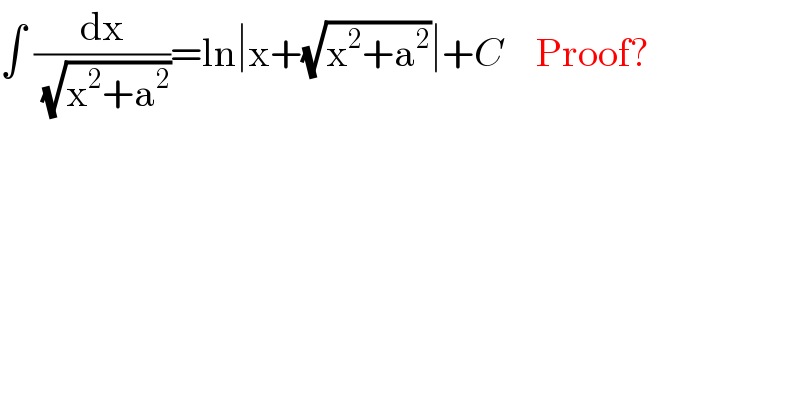
∫ (dx/( (√(x^2 +a^2 ))))=ln∣x+(√(x^2 +a^2 ))∣+C Proof?
$$\int\:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}=\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mid+{C}\:\:\:\:\mathrm{Proof}? \\ $$
Answered by bobhans last updated on 23/Aug/20
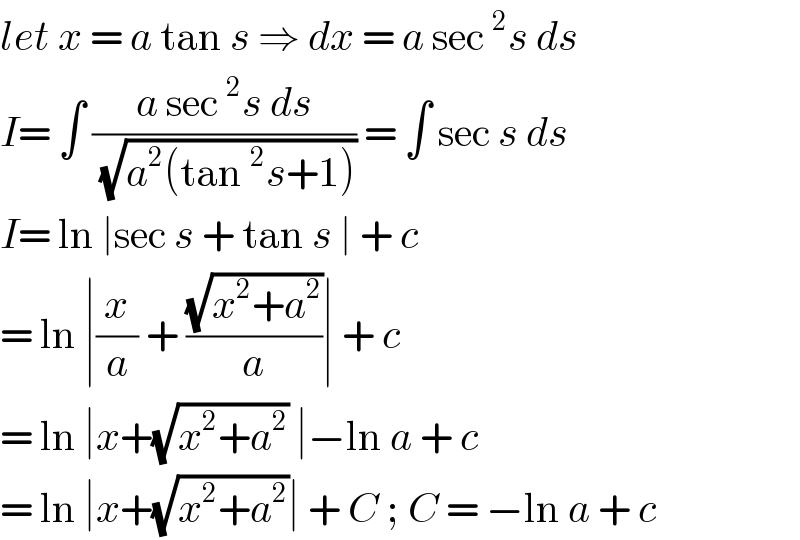
let x = a tan s ⇒ dx = a sec^2 s ds I= ∫ ((a sec^2 s ds)/( (√(a^2 (tan^2 s+1))))) = ∫ sec s ds I= ln ∣sec s + tan s ∣ + c = ln ∣(x/a) + ((√(x^2 +a^2 ))/a)∣ + c = ln ∣x+(√(x^2 +a^2 )) ∣−ln a + c = ln ∣x+(√(x^2 +a^2 ))∣ + C ; C = −ln a + c
$${let}\:{x}\:=\:{a}\:\mathrm{tan}\:{s}\:\Rightarrow\:{dx}\:=\:{a}\:\mathrm{sec}\:^{\mathrm{2}} {s}\:{ds}\: \\ $$$${I}=\:\int\:\frac{{a}\:\mathrm{sec}\:^{\mathrm{2}} {s}\:{ds}}{\:\sqrt{{a}^{\mathrm{2}} \left(\mathrm{tan}\:^{\mathrm{2}} {s}+\mathrm{1}\right)}}\:=\:\int\:\mathrm{sec}\:{s}\:{ds}\: \\ $$$${I}=\:\mathrm{ln}\:\mid\mathrm{sec}\:{s}\:+\:\mathrm{tan}\:{s}\:\mid\:+\:{c} \\ $$$$=\:\mathrm{ln}\:\mid\frac{{x}}{{a}}\:+\:\frac{\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}{{a}}\mid\:+\:{c} \\ $$$$=\:\mathrm{ln}\:\mid{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\:\mid−\mathrm{ln}\:{a}\:+\:{c}\: \\ $$$$=\:\mathrm{ln}\:\mid{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\mid\:+\:{C}\:;\:{C}\:=\:−\mathrm{ln}\:{a}\:+\:{c}\: \\ $$
Answered by 1549442205PVT last updated on 23/Aug/20
Since ∣x+(√(x^2 +a^2 )) ∣=x+(√(x^2 +a^2 )) (due to x+(√(x^2 +a^2 )) >0 ∀x∈R),so we have (d/dx)(ln∣x+(√(x^2 +a^2 ))∣+C)=(d/dx)[ln(x+(√(x^2 +a^2 )))] =(1/(x+(√(x^2 +a^2 ))))×(d/dx)(x+(√(x^2 +a^2 )) )= =(1/(x+(√(x^2 +a^2 ))))×(1+(x/( (√(x^2 +a^2 ))))) =(1/(x+(√(x^2 +a^2 ))))×((x+(√(x^2 +a^2 )))/( (√(x^2 +a^2 ))))=(1/( (√(x^2 +a^2 )))) This shows that ∫(dx/( (√(x^2 +a^2 ))))=ln∣x+(√(x^2 +a^2 ))∣+C (Q.E.D)
$$\mathrm{Since}\:\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\:\mid=\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \:}\:\left(\mathrm{due}\right. \\ $$$$\left.\mathrm{to}\:\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \:}\:>\mathrm{0}\:\forall\mathrm{x}\in\mathrm{R}\right),\mathrm{so}\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mid+{C}\right)=\frac{\mathrm{d}}{\mathrm{dx}}\left[\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}×\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\:\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}×\left(\mathrm{1}+\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}×\frac{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }} \\ $$$$\mathrm{This}\:\mathrm{shows}\:\mathrm{that} \\ $$$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }}=\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }\mid+\mathrm{C}\:\left(\boldsymbol{\mathrm{Q}}.\boldsymbol{\mathrm{E}}.\boldsymbol{\mathrm{D}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *