Question Number 174951 by infinityaction last updated on 14/Aug/22
![lim_(n→∞) (1/n)[1+(√2)+^3 (√3)+...^n (√n)]](https://www.tinkutara.com/question/Q174951.png)
$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\left[\mathrm{1}+\sqrt{\mathrm{2}}+^{\mathrm{3}} \sqrt{\mathrm{3}}+…^{{n}} \sqrt{{n}}\right] \\ $$
Answered by TheHoneyCat last updated on 16/Aug/22

$$\mathrm{There}'\mathrm{s}\:\mathrm{a}\:\mathrm{theorem}\:\mathrm{that}\:\mathrm{sates}\:\mathrm{that} \\ $$$${U}_{{n}} \:\:\underset{{n}\rightarrow\infty} {\rightarrow}{l}\:\in\:\overset{\_} {\mathbb{R}}\:\Rightarrow\:\mathrm{lim}_{{n}\rightarrow\infty} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{U}_{{k}} ={l} \\ $$$$ \\ $$$$\mathrm{Now} \\ $$$$\:^{{n}} \sqrt{{n}}={n}^{\mathrm{1}/{n}} =\mathrm{exp}\left(\frac{\mathrm{ln}\:{n}}{{n}}\right)\: \\ $$$$\mathrm{since}\:\mathrm{ln}\:{n}\:/{n}\rightarrow\mathrm{0} \\ $$$$\:^{{n}} \sqrt{{n}}\rightarrow\mathrm{exp}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Thus}:\: \\ $$$$\mathrm{your}\:\mathrm{limit}\:\mathrm{is}\:\mathrm{1}. \\ $$
Commented by TheHoneyCat last updated on 16/Aug/22
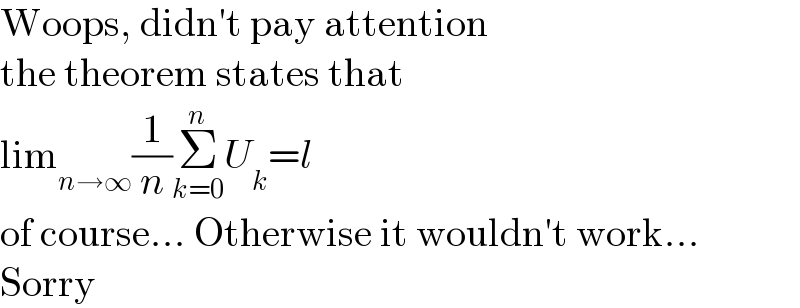
$$\mathrm{Woops},\:\mathrm{didn}'\mathrm{t}\:\mathrm{pay}\:\mathrm{attention} \\ $$$$\mathrm{the}\:\mathrm{theorem}\:\mathrm{states}\:\mathrm{that}\: \\ $$$$\mathrm{lim}_{{n}\rightarrow\infty} \frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{U}_{{k}} ={l} \\ $$$$\mathrm{of}\:\mathrm{course}…\:\mathrm{Otherwise}\:\mathrm{it}\:\mathrm{wouldn}'\mathrm{t}\:\mathrm{work}… \\ $$$$\mathrm{Sorry} \\ $$
